
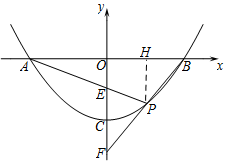
【题目】抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
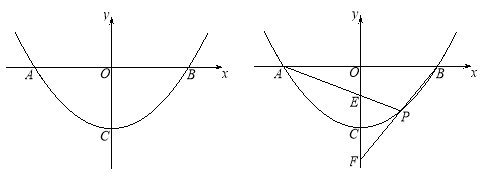
【答案】(1)①y=![]() x2-
x2-![]() ;②点D的坐标为(-1,-3)或(
;②点D的坐标为(-1,-3)或(![]() ,
,![]() );(2)是定值,等于2.
);(2)是定值,等于2.
【解析】
试题分析:(1)①将P(1,-3)、B(4,0)代入y=ax2+c得方程组,解方程组即可求得a、c的值,就求得函数解析式;②分两种情况求得点D的坐标即可;(2)设B(b,0),则A(-b,0)有ab2+c=0,即可得b2=![]() ,过点P(x0,y0)作PH⊥AB,有
,过点P(x0,y0)作PH⊥AB,有![]() ,利用相似三角形的性质分别求得OE、OF的值,即可得
,利用相似三角形的性质分别求得OE、OF的值,即可得![]() 的值.
的值.
试题解析:(1)①将P(1,-3)、B(4,0)代入y=ax2+c得
![]() ,解得
,解得 ,抛物线的解析式为:
,抛物线的解析式为:![]() .
.
②如图:
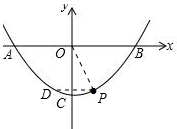
由∠DPO=∠POB得DP∥OB,D与P关于y轴对称,P(1,-3)得D(-1,-3);
如图,D在P右侧,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,
设Q(q,0),则(q-1)2+32=q2,解得:q=5,∴Q(5,0),则直线PD2为![]() ,再联立
,再联立 得:x=1或
得:x=1或![]() ,∴ D2(
,∴ D2(![]() )
)
∴点D的坐标为(-1,-3)或(![]() )
)
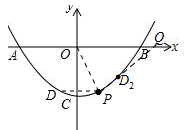
(2)设B(b,0),则A(-b,0)有ab2+c=0,∴b2=![]() ,过点P(x0,y0)作PH⊥AB,有
,过点P(x0,y0)作PH⊥AB,有![]() ,易证:△PAH∽△EAO,则
,易证:△PAH∽△EAO,则 ![]() 即
即![]() ,∴
,∴![]() ,
,
同理得![]() ∴
∴![]() ,∴
,∴![]() ,则OE+OF=
,则OE+OF=![]()
∴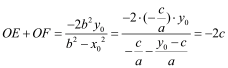 ,又OC=-c,∴
,又OC=-c,∴![]() .
.
∴![]() 是定值,等于2.
是定值,等于2.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】对于一组数据:x1,x2,x3,…,x10,若去掉一个最大值和一个最小值,则下列统计量一定不会发生变化的是( )
A.平均数B.中位数C.众数D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2﹣6x+c与x轴交于点A(﹣5,0)、B(﹣1,0),与y轴交于点C(0,﹣5),点P是抛物线上的动点,连接PA、PC,PC与x轴交于点D.
(1)求该抛物线所对应的函数解析式;
(2)若点P的坐标为(﹣2,3),请求出此时△APC的面积;
(3)过点P作y轴的平行线交x轴于点H,交直线AC于点E,如图2.
①若∠APE=∠CPE,求证:=;
②△APE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
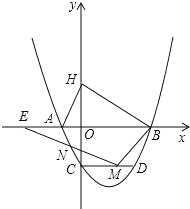
【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(4,0),与y轴交于C(0,﹣2).
(1)求抛物线的解析式;
(2)H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);
(3)过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
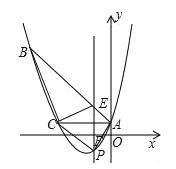
【题目】(2016山东潍坊第25题)如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人的大脑每天能记录大约8 600万条信息,数据8 600用科学记数法表示为( )
A.0.86×104
B.8.6×102
C.8.6×103
D.86×102
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com