
【题目】如图,在Rt△ABC中,∠A=90°,点D、E分别在AC、BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB、BC分别交于点F、G.
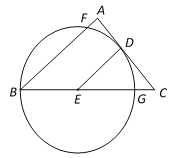
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,求⊙E的半径;
(3)若Rt△ABC的内切圆圆心为I,求⊙I的面积.
【答案】(1)证明见解析;(2)⊙E的半径为20;(3)130π.
【解析】(1)证明△CDE∽△CAB,得∠EDC=∠A=90°,所以AC是⊙E的切线;
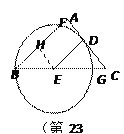
(2)如图1,作辅助线,构建矩形AHED,设⊙E的半径为r,表示BH和EC的长,证明△BHE∽△EDC,列比例式代入r可得结论;
(3)如图2,作辅助线,构建直角△IME,分别求IM和ME的值,利用勾股定理可求IE的长.
(1)∵ CD·BC=AC·CE,
∴![]() =
=![]()
∵∠DCE=∠ACB.
∴△CDE∽△CAB,
∴∠EDC=∠A=90° ,
∴ED⊥AC
又∵点D在⊙O上,
∴AC与⊙E相切于点D .
(2)过点E作EH⊥AB,垂足为H,
∴BH=FH.
在四边形AHED中,∠AHE=∠A=∠ADE=90°,
∴四边形AHED为矩形,
∴ED=HA,ED∥AB,
∴∠B=∠DEC.
设⊙O的半径为r,则EB=ED=EG=r,
∴BH=FH=r-4,EC=r+5.
在△BHE和△EDC中,
∵∠B=∠DEC,∠BHE=∠EDC,
∴△BHE∽△EDC.
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∴r=20.即⊙E的半径为20.
(3)如图2,过I作IM⊥BC于M,过I作IH⊥AB于H,
由①得:FH=BH=r-4=20-4=16,AB=AF+2BH=4+2×16=36,
BC=2r+5=2×20+5=45,
∴AC= ![]() =27,
=27,
∵I是Rt△ABC的内心,
∴IM=(AB+ACBC) ÷2=(36+2745) ÷2=9,
∴AH=IM=9,
∴BH=BM=36-9=27,
∴EM=27-20=7,
在Rt△IME中,由勾股定理得:IE= ![]() , .
, .
∴⊙I的面积=π×![]() =130π.
=130π.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】某游泳池普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常销售,两种优惠卡仅限暑假使用,每人一次一张票不限次数.
(1)分别写出选择普通票、银卡消费时,所需费用![]() 、
、![]() 与次数
与次数![]() 之间的函数表达式;
之间的函数表达式;
(2)小明打算暑假每天游泳一次,按55天计算,则选择哪种消费方式更合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套房子,他准备将地面都铺上地砖,地面结构如图所示,请根据图中的数据(单位:米),解答下列问题:
(1)用含x,y的代数式表示地面总面积为 平方米;
(2)若x=5,y=1,铺地砖每平方米的平均费用为100元,则铺地砖的总费用为 元;
(3)已知房屋的高度为3米,现需要在客厅和卧室的墙壁上贴壁纸,那么用含x的代数式表示至少需要 平方米的壁纸;如果所粘壁纸的价格是100元/平方米,那么用含x的代数式表示购买该壁纸至少需要 元.(计算时不扣除门,窗所占的面积)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数![]() ,可以组成两个有理数对
,可以组成两个有理数对![]() 与
与![]() .
.
我们规定:![]() .
.
例如:![]() .
.
根据上述规定解决下列问题:
(1)有理数对![]() ;
;
(2)若有理数对![]() ,则
,则![]() ;
;
(3)当满足等式![]() 的
的![]() 是整数时,求整数
是整数时,求整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组连续奇数按如图方式排列,请你解决下列问题:

![]() 第
第![]() 行最后一个数字是___________,在第
行最后一个数字是___________,在第![]() 行第
行第![]() 列的数字是_______________
列的数字是_______________
![]() 请用含
请用含![]() 的代数式表示第
的代数式表示第![]() 行的第
行的第![]() 个数字和最后一个数字;
个数字和最后一个数字;
![]() 现用一个正方形框去围出相邻两行中的
现用一个正方形框去围出相邻两行中的![]() 个数字(例如:第
个数字(例如:第![]() 行和第
行和第![]() 行的
行的![]() ),请问能否在第
),请问能否在第![]() 行和第
行和第![]() 行中求出
行中求出![]() 个数字的和是
个数字的和是![]() ?若能,请求出这
?若能,请求出这![]() 个数字;若不能,请说明理由.
个数字;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
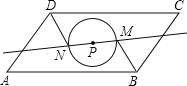
【题目】如图,P为平行四边形ABCD的对称中心,以P为圆心作圆,过P的任意直线与圆相交于点M,N.则线段BM,DN的大小关系是( )
A. BM>DN B. BM<DN C. BM=DN D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() (实数m是常数).
(实数m是常数).
(1)若x+y=1,求实数m的值;
(2)若-1≤x-y≤5,求m的取值范围;
(3)在(2)的条件下,化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
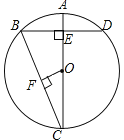
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com