
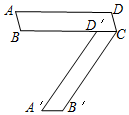
 将平行四边形ABCD(如图)绕点C旋转后,点D落在边BC上的点D′,点A落到A′,且点A′、B、A在一直线上.如果AB=3,AD=13,那么cos A=$\frac{5}{13}$.
将平行四边形ABCD(如图)绕点C旋转后,点D落在边BC上的点D′,点A落到A′,且点A′、B、A在一直线上.如果AB=3,AD=13,那么cos A=$\frac{5}{13}$. 分析 根据平行四边形的性质得∠DCB=∠D′CB′,CB=CB′=C′D′=13,再由CB′∥A′D′得∠D′CB′=∠BD′A′,根据平行线的性质得到∠C=∠C′BD′,推出△A′BD′为等腰三角形,作A′H⊥D′B,根据等腰三角形的性质得BH=D′H,由于BD′=10得到D′H=5,然后根据余弦的定义即可得到结论.
解答  解:∵?ABCD绕点C旋转后得到?A′B′CD′,
解:∵?ABCD绕点C旋转后得到?A′B′CD′,
∴∠DCB=∠D′CB′,CB=CB′=A′D′=13,
∵CB′∥A′D′,
∴∠D′CB′=∠BD′A′,
∵四边形ABCD为平行四边形,
∴∠A=∠DCB,
∴∠A=∠BD′A′,
∵点A′、B、A在一直线上,
而CB∥AD,
∴∠A=∠A′BD′,
∴∠A′BD′=∠BD′A′,
∴△A′BD′为等腰三角形,
作A′H⊥D′B,则BH=D′H,
∵CB=13,AB=3,
∴BD′=10,
∴D′H=5,
∴cos∠HD′A′=$\frac{D′H}{D′A′}$=$\frac{5}{13}$,
即cos A=$\frac{5}{13}$.
故答案为$\frac{5}{13}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的性质.解决本题的关键是证明△C′BD′为等腰三角形.


科目:初中数学 来源: 题型:解答题
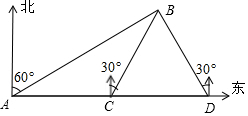 如图,某货轮上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到到达C,D处的时间.
如图,某货轮上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到到达C,D处的时间.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
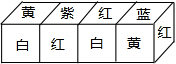 把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:| 颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
| 花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
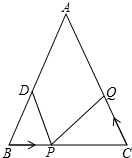 如图,△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C移动,同时,点Q在线段CA上由点C向点A移动.若点Q的移动速度与点P的移动速度相同,则经过1秒后,△BPD≌△CQP.
如图,△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C移动,同时,点Q在线段CA上由点C向点A移动.若点Q的移动速度与点P的移动速度相同,则经过1秒后,△BPD≌△CQP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com