
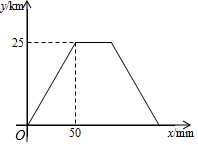
 甲、乙两人骑车分别从A、B两地同时出发,沿同一路线匀速骑行,两人先相向而行,甲到达B地后停留20min再以原速返回A地,当两人到达A地后停止骑行.设甲出发xmin后距离A地的路程为ykm.图中的折线表示甲在整个骑行过程中y与x的函数关系.
甲、乙两人骑车分别从A、B两地同时出发,沿同一路线匀速骑行,两人先相向而行,甲到达B地后停留20min再以原速返回A地,当两人到达A地后停止骑行.设甲出发xmin后距离A地的路程为ykm.图中的折线表示甲在整个骑行过程中y与x的函数关系.分析 (1)由y的最大值为25,即可得出A、B两地之间的路程为25km;
(2)先根据速度=路程÷时间求出甲骑车的速度,再结合甲到达B地的时间结合停留的时间找出甲从B地出发到A地的初始时间,最后利用路程=25-速度×时间,即可求出甲从B地返回A地时,y与x的函数表达式;
(3)由二者只相遇一次,可得出乙到达A所用的时间t<120,再根据速度=路程÷时间,即可求出乙骑行速度的取值范围,对照四个选项即可得出结论.
解答 解:(1)观察函数图象,可知:A、B两地之间的路程是25km.
故答案为:25.
(2)∵甲从A地到B地的速度为25÷50=0.5(km/min),
∴甲从B地返回A地的速度也为0.5km/min.
∵甲到达B地后停留20min再以原速返回A地,
∴甲从B地返回A地时已出发70分钟,且距离A地25km,
∴y=25-0.5(x-70)=60-0.5x.
(3)当y=60-0.5x=0时,x=120.
∵在整个骑行过程中,两人只相遇了1次,
∴乙到达A所用的时间t<120,
又∵乙的骑行速度v=$\frac{25}{t}$,
∴t>$\frac{5}{24}$≈0.21.
故答案为:D.
点评 本题考查了一次函数的应用,解题的关键是:(1)观察函数图象,找出两地间的距离;(2)根据路程=25-速度×时间,找出y关于x的函数关系式;(3)利用速度=路程÷时间,求出乙骑行速度的取值范围.


科目:初中数学 来源: 题型:解答题
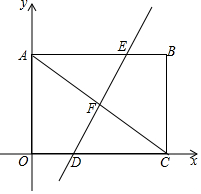 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
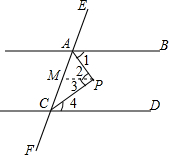 已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数.
已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com