
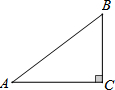
 如图,△ABC中∠ACB=90°,AC=8cm,BC=6cm
如图,△ABC中∠ACB=90°,AC=8cm,BC=6cm分析 (1)以A,B为圆心,以大于AB长度的一半为半径画弧,两弧交于两点,过两点作直线即为所求;
(2)由勾股定理求出AB的长度,通过三角形相似列比例式即可得到结果.
解答 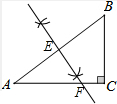 解:(1)如图所示,直线EF即为所求;
解:(1)如图所示,直线EF即为所求;
(2)∵∠ACB=90°,AC=8cm,BC=6cm
∴AB=$\sqrt{{AC}^{2}{+BC}^{2}}$=10cm,
∵EF垂直平分AB,
∴AE=$\frac{1}{2}$AB=5cm,
∵∠A=∠A,∠AEF=∠C=90°,
∴△AEF∽△ACB,
∴$\frac{EF}{BC}$=$\frac{AE}{AC}$,
∴$\frac{EF}{6}$=$\frac{5}{8}$,则EF=$\frac{15}{4}$cm.
点评 本题考查了基本作图,解直角三角形,相似三角形的判定和性质,掌握线段垂直平分线的性质是解题的关键.


科目:初中数学 来源: 题型:填空题
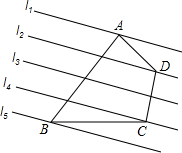 如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是$\frac{17}{2}$.
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是$\frac{17}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | (-$\sqrt{3}$)2=9 | C. | $\root{3}{-9}$=-3 | D. | ±$\sqrt{9}$=±3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 下列不等式组的解集,在数轴上表示为如图所示的是( )
下列不等式组的解集,在数轴上表示为如图所示的是( )| A. | $\left\{\begin{array}{l}{x-1>0}\\{x+2≤0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1>0}\\{x-2≤0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+1≥0}\\{x-2<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-1≤0}\\{x+2<0}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
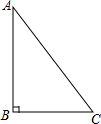 如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )
如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )| A. | $\frac{7}{sin40°}$ | B. | $\frac{7}{tan40°}$ | C. | 7cos40° | D. | $\frac{7}{cos40°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| B. | 数据1、2、2、3的平均数是2 | |
| C. | 数据5、2、-3、0的极差是8 | |
| D. | 如果某种游戏活动的中奖率为40%,那么参加这种活动10次一定有4次中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18 | B. | $\sqrt{6}$ | C. | $3\sqrt{2}$ | D. | ±$3\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com