某商场计划拨款9万元从厂家购买50台电视机,已知该厂家生产三种不同型号的电视机的出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元,商场销售一台甲种电视机可获利150元,销售乙种电视机每台可获利200元,销售丙种电视机每台可获利250元.
(1)若同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)经市场调查这三种型号的电视机是最受欢迎的,且销售量乙种是丙种的3倍.商场要求成本不能超过计划拨款数额,利润不能少于8500元的前提,购进这三种型号的电视机共50台,请你设计这三种不同型号的电视机各进多少台?
【答案】
分析:(1)根据题意得出:两个等量关系:两种不同型号电视机共50台,花费90000元,分情况讨论:①购进甲型号电视机和乙型号电视机②设购进丙型号电视机和乙型号电视机③设购进甲型号电视机和丙型号电视机,分别求出结果.
(2)根据题意设出未知数,设购进丙型号电视机s台,则购进乙型号电视机3s台,购进甲型号电视机(50-4s)台,再找出题目中列不等式的关键词:①成本不能超过计划拨款数额,②利润不能少于8500元,解不等式组可得答案.
解答:解:(1)①设购进甲型号电视机x台,乙型号电视机y台,由题意得:
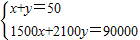
,
解得:

,
②设购进丙型号电视机m台,乙型号电视机n台,由题意得:
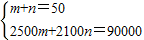
,
解得:m,n不是整数,所以舍去,不合题意.
③设购进甲型号电视机a台,丙型号电视机b台由题意得:
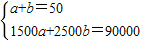
,
解得:
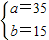
,
∴进货方案有两种:
①购进甲型号电视机25台,乙型号电视机25台,
②购进甲型号电视机35台,丙型号电视机15台,
(2)设购进丙型号电视机s台,则购进乙型号电视机3s台,购进甲型号电视机(50-4s)台,由题意得:
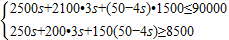
,
解得:4≤s≤5
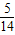
,
∵s为整数,
∴s=4或5,
当s=4时:购进乙型号电视机12台,购进甲型号电视机34台,
s=5时:购进乙型号电视机15台,购进甲型号电视机30台,
答:购进方案有两种:①购进丙型号电视机4台,则购进乙型号电视机12台,购进甲型号电视机34台,
②购进丙型号电视机5台,则购进乙型号电视机15台,购进甲型号电视机30台.
点评:此题主要考查了二元一次方程组的应用,不等式组的应用,解决此题的关键是弄懂题意,设出未知数,理清数量之间的关系后,①找出列方程组的相等关系,②找出列不等式组的不等关系.

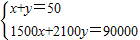 ,
, ,
,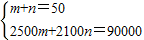 ,
,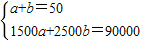 ,
,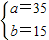 ,
,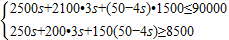 ,
,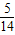 ,
,

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案