
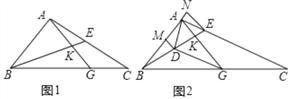
【题目】如图1,已知△ABC中,∠ABC=45°,点E为AC上的一点,连接BE,在BC上找一点G,使得AG=AB,AG交BE于K.
(1)若∠ABE=30°,且∠EBC=∠GAC,BK=4,求AC的长度.
(2)如图2,过点A作DA⊥AE交BE于点D,过D、E分别向AB所在的直线作垂线,垂足分别为点M、N,且NE=AM,若D为BE的中点,证明: ![]() DG=2AG.
DG=2AG.
【答案】(1)AC=2![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)如图1中,作AH⊥BG于H.在Rt△ABK中,求出AK、AB.在Rt△ABH中,求出AH.在Rt△AHC中,证明∠C=30°,即可推出AC=2AH,由此解决问题.
(2)如图2中,连接EG.由△MAD≌△NEA,推出AD=AE再证明△BAD≌△GAE,推出BD=EG=DE,∠ABD=∠AGE,推出DGE是等腰直角三角形,设AD=AE=a,求出DG、AG即可解决问题.
试题解析:解:(1)如图1中,作AH⊥BG于H.
在Rt△ABK中,∵∠BAK=90°,∠ABK=30°,BK=4,∴AK=![]() BK=2,AB=
BK=2,AB=![]() =
=![]() .∵AB=AG,∠BAC=90°,∴∠ABC=∠AGB=45°,∠CBE=∠CAG=15°.∵∠AGB=∠C+∠CAG,∴∠C=30°.在Rt△AHC中,∵∠AHC=90°,∠C=30°,∴AC=2AH.在Rt△ABH中,AH=BH=
.∵AB=AG,∠BAC=90°,∴∠ABC=∠AGB=45°,∠CBE=∠CAG=15°.∵∠AGB=∠C+∠CAG,∴∠C=30°.在Rt△AHC中,∵∠AHC=90°,∠C=30°,∴AC=2AH.在Rt△ABH中,AH=BH=![]() AB=
AB=![]() ,∴AC=
,∴AC=![]() .
.

(2)如图2中,连接EG.∵DM⊥AB,EN⊥BA,∴∠AMD=∠N=∠DAE=90°,∴∠MAD+∠NAE=90°,∠NAE+∠NEA=90°,∴∠MAD=∠NEA.
在△MAD和△NEA中,∵∠MAD=∠AEN,AM=NE,∠AMD=∠NEA,∴△MAD≌△NEA,∴AD=AE.∵∠BAC=∠DAE=90°,∴∠BAD=∠GAE.
在△BAD和△GAE中,∵BA=AG,∠BAD=∠GAE,AD=AE,∴△BAD≌△GAE,∴BD=EG=DE,∠ABD=∠AGE.∵∠AKB=∠EKG,∴∠KEG=∠KAB=90°,∴△DGE是等腰直角三角形.设AD=AE=a,∴∠ADE=∠EDG=45°,∴∠ADG=90°,∴DE=BD=EG=![]() a,DG=
a,DG=![]() DE=2a.
DE=2a.
在Rt△ADG中,AG=![]() =
= ![]() ,∴
,∴![]() ,∴
,∴![]() DG=2AG.
DG=2AG.



科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在方程ax=12(a是正整数)中,x是未知数,a是用字母表示的已知数。于是,在项ax中,字母a是_____________,我们把a叫做_____________。这个方程是含有系数的_____________。在方程![]() 中,
中,![]() 是未知数,b和s是用字母表示的已知数。同样地,字母b是______________字母s也叫做__________________,这个方程是含有系数的_____________。
是未知数,b和s是用字母表示的已知数。同样地,字母b是______________字母s也叫做__________________,这个方程是含有系数的_____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC上一点,BE![]() BC,连接AE,作BF⊥AE,分别与AE、CD交于点K、F,G、H分别在AD、AE上,且四边形KFGH是矩形,则
BC,连接AE,作BF⊥AE,分别与AE、CD交于点K、F,G、H分别在AD、AE上,且四边形KFGH是矩形,则![]() ________.
________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(-1,0),B(4,0),与y轴交于C(0,-2).(1)求抛物线的解析式;
(2)H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);
(3)过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
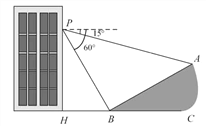
【题目】如图,小明在大楼45米高(即PH=45米,且PH⊥HC)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的
坡度i(即tan∠ABC)为1: ![]() .(点P、H、B、C、A在同一个平面上
.(点P、H、B、C、A在同一个平面上
点H、B、C在同一条直线上)
(1)∠PBA的度数等于________度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732).
≈1.732).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com