
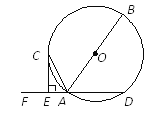
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF.
(1)求证:AC平分∠FAB;
(2)若AE=1,CE=2,求⊙O的半径.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OC,根据切线的性质和圆周角定理,得出∠OCA=∠OAC与∠CAE=∠OCA,然后根据角平分线的定义可证明;
(2)由圆周角定理得到∠BCA=90°,由垂直的定义,可求出∠CEA=90°,从而根据两角对应相等的两三角形相似可证明△ACB∽△AEC,再根据相似三角形的对应边成比例求得AB的长,从而得到圆的半径.
试题解析:(1)证明:连接OC.
∵CE是⊙O的切线,∴∠OCE =90°
∵CE⊥DF,∴∠CEA=90°,
∴∠ACE+∠CAE=∠ACE+∠OCA=90°,∴∠CAE=∠OCA
∵OC=OA,∴∠OCA=∠OAC.
∴∠CAE=∠OAC,即AC平分∠FAB
(2)连接BC.
∵AB是⊙O的直径,∴∠ACB =∠AEC =90°.
又∵∠CAE=∠OAC,∴△ACB∽△AEC,∴![]() .
.
∵AE=1,CE=2,∠AEC =90°,∴![]()
∴ ,∴⊙O的半径为
,∴⊙O的半径为![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() <
<![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
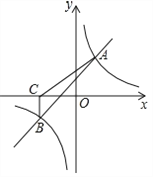
【题目】如图,已知直线y=﹣2x+12分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的⊙M与直线AB相切于点D,连接MD.
(1)求证:△ADM∽△AOB;
(2)如果⊙M的半径为2![]() ,请写出点M的坐标,并写出以(﹣
,请写出点M的坐标,并写出以(﹣![]() ,
, ![]() )为顶点,且过点M的抛物线的解析式.
)为顶点,且过点M的抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数![]() 、
、![]() 之间的一种运算,记作(
之间的一种运算,记作(![]() ,
,![]() );如果
);如果![]() ,那么(
,那么(![]() ,
,![]() )=c.
)=c.
例如:因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:(4,16)=_________,(7,1)=___________,(_______,![]() )=-2.
)=-2.
(2)小明在研究这种运算时发现一个现象:(![]() ,
,![]() )=(3,4)小明给出了如下的证明:
)=(3,4)小明给出了如下的证明:
设(![]() ,
,![]() )=
)=![]() ,则
,则![]() ,即
,即![]()
所以![]() ,即(3,4)=
,即(3,4)=![]() ,
,
所以(![]() ,
,![]() )=(3,4).
)=(3,4).
请你尝试运用这种方法解决下列问题:
①证明:(6,45)-(6,9)=(6,5)
②猜想:(![]() ,
,![]() )+(
)+(![]() ,
,![]() )=(____________,____________),(结果化成最简形式).
)=(____________,____________),(结果化成最简形式).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(-3,0),B(0,-1),C(0,![]() )三点.
)三点.
(1)求直线AB的解析式.
(2)若点D在直线AB上,且DB=DC,尺规作图作出点D(保留作图痕迹),并求出点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三名射箭运动员在某次测试中各射箭8次,三人的测试成绩如下表:
s2甲、s 2乙、s 2丙分别表示三名运动员这次测试成绩的方差,下面各式中正确的是( )

A. s 2甲>s 2乙>s 2丙 B. s 2丙>s 2乙>s 2甲
C. s 2丙>s 2甲>s 2乙 D. s 2乙>s 2甲>s 2丙
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() .
.
(1)在如图所示的平面直角坐标系中描出各点,画出![]() ;
;
(2)将![]() 先向左平移3个单位长度,再向下平移5个单位长度,得到
先向左平移3个单位长度,再向下平移5个单位长度,得到![]() , 请画出
, 请画出![]()
(3)求![]() 的面积;
的面积;
(4)设点![]() 在坐标轴上,且
在坐标轴上,且![]() 与
与![]() 的面积相等,请直接写出
的面积相等,请直接写出![]() 点的坐标
点的坐标

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com