
 正三角形ADE,当△ABC的面积是25
正三角形ADE,当△ABC的面积是25 ,△ADE的面积是7
,△ADE的面积是7 时,BD与DC的比值是
时,BD与DC的比值是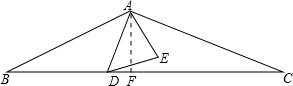
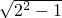 AF=
AF= AF.
AF. ×BC×AF=25
×BC×AF=25 ,计算得:AF=5,BF=5
,计算得:AF=5,BF=5 .
.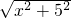 ,
, AD×(
AD×(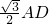 )=
)= AD2=7
AD2=7 ,
, ,
, ,CD=CF+FD=6
,CD=CF+FD=6 ,
,

科目:初中数学 来源: 题型:
 8、
8、 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:
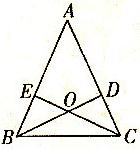 25、如图所示,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点0,给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.
25、如图所示,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点0,给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.查看答案和解析>>
科目:初中数学 来源: 题型:
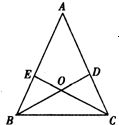 17、如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定
17、如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC在平面直角坐标系中的位置如图,有以下五个结论:①点A的坐标是(0,3);②把△ABC向左平移三个单位后,点B的对应点在函数y=-
如图,已知△ABC在平面直角坐标系中的位置如图,有以下五个结论:①点A的坐标是(0,3);②把△ABC向左平移三个单位后,点B的对应点在函数y=-| 8 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在△ABC中,∠ACB=90°,点A的坐标为(0,2),点B(-3,1)在抛物线y=ax2+ax-2上,点C在x轴上.
在△ABC中,∠ACB=90°,点A的坐标为(0,2),点B(-3,1)在抛物线y=ax2+ax-2上,点C在x轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com