
 在矩形ABCD中,AB=6,BC=7,E、F、M分别为AB、BC、CD边上的点,连接EF、FM、ME,且AE=3,DM=2,若∠EFM=90°,BF>FC,则BF=( )
在矩形ABCD中,AB=6,BC=7,E、F、M分别为AB、BC、CD边上的点,连接EF、FM、ME,且AE=3,DM=2,若∠EFM=90°,BF>FC,则BF=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 由四边形ABCD是矩形,得到∠B=∠C=90°,CD=AB=6,根据AE=3,DM=2,于是得到BE=3,CM=4,推出△BEF∽△CFM,得到关于BF的比例式,即可得出答案,
解答 解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD=AB=6,
∵AE=3,DM=2,
∴BE=3,CM=4,
∵EF⊥FM,
∴∠BEF+∠BFE=∠BFE+∠MFC=90°,
∴∠BEF=∠CFM,
∴△BEF∽△CFM,
∴$\frac{BF}{CM}=\frac{BE}{CF}$,即$\frac{BF}{4}=\frac{3}{7-BF}$,
解得:BF=4,或BF=3(舍去),
∴BF=4;
故选:B.
点评 本题考查了相似三角形的判定和性质,矩形的性质,熟练掌握相似三角形的判定和性质定理是解题的关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:选择题
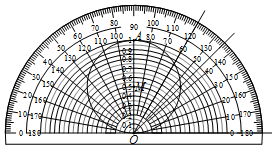 利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )
利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:sin60°≈0.87,sin45°=0.71.下列角度中正弦值最接近0.94的是( )| A. | 70° | B. | 50° | C. | 40° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
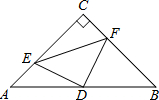 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
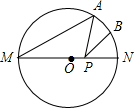 如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>3 | B. | m≥3 | C. | m=3 | D. | m<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com