
【题目】如图四边形ABCD内接于⊙O ,BD是⊙O 的直径,AE⊥CD,垂足为E,DA平分∠BDE.
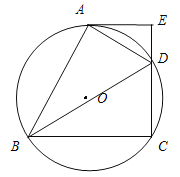
(1)求证:AE是⊙O 的切线;
(2)若∠DBC=30°,DE=1cm,求BD的长.
【答案】(1)见解析(2)BD=4cm
【解析】
试题分析:(1)连接OA ,根据条件证明OA∥DE,然后得出AE⊥OA即可得出结论;(2)结合(1)的结论得出∠EAD=∠ABD=30°,然后在Rt△AED中求出AD的长,然后在Rt△ABD中可求出BD的长.
试题解析:(1)连接OA ,
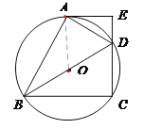
∵AO=OD ,
∴∠OAD=∠ODA ,
∵∠ODA=∠EDA,
∴∠EDA=∠OAD
∴OA∥DE
∵AE⊥CD ,
∴AE⊥OA
∴DE是⊙O的切线
(2)∵BD是⊙O的直径,∠DBC=30°
∴∠BCD=∠BAD=90°,∠BDC=60°
由(1)知,∠ODA=∠EDA=60°
∴∠EAD=∠ABD=30°
在Rt△AED中, AD=2DE=2cm
∴BD=4cm


科目:初中数学 来源: 题型:
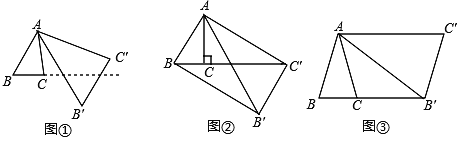
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′ ,如图①所示,∠BAB′ =θ, ![]() ,我们将这种变换记为[θ,n] .
,我们将这种变换记为[θ,n] .
(1)如图①,对△ABC作变换[60°,![]() ]得到△AB′C′ ,则
]得到△AB′C′ ,则![]() :
:![]() = ;直线BC与直线B′C′所夹的锐角为 度;
= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、![]() 在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆重新装修后,准备在大厅的主楼梯上铺设某种红地毯,已知这种地毯售价为30元/m2 , 主楼梯宽2m,其侧面如图所示.
(1)求这个地毯的长是多少?
(2)求这个地毯的面积是多少平方米?
(3)求购买地毯至少需要多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形的外心是( )
A. 三角形三条边上中线的交点B. 三角形三条边上高线的交点
C. 三角形三条边垂直平分线的交点D. 三角形三条内角平分线的交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com