
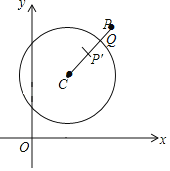
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOy ÖŠ£¬µćPŹĒ”ŃCĶāŅ»µć£¬Į¬½ÓCP½»”ŃCÓŚµćQ£¬µćP¹ŲÓŚµćQµÄ¶Ō³ĘµćĪŖP”䣬µ±µćP”äŌŚĻ߶ĪCQÉĻŹ±£¬³ĘµćPĪŖ”ŃC”°ÓŃŗƵ攱£®ŅŃÖŖA£Ø1£¬0£©£¬B£Ø0£¬2£©£¬C£Ø3£¬3£©
£Ø1£©µ±”ŃOµÄ°ė¾¶ĪŖ1Ź±£¬
¢ŁµćA£¬B£¬CÖŠŹĒ”ŃO”°ÓŃŗƵ攱µÄŹĒ”” ””£»
¢ŚŅŃÖŖµćMŌŚÖ±Ļßy£½©![]() x+2 ÉĻ£¬ĒŅµćMŹĒ”ŃO”°ÓŃŗƵ攱£¬ĒóµćMµÄŗį×ų±źmµÄȔֵ·¶Ī§£»
x+2 ÉĻ£¬ĒŅµćMŹĒ”ŃO”°ÓŃŗƵ攱£¬ĒóµćMµÄŗį×ų±źmµÄȔֵ·¶Ī§£»
£Ø2£©ŅŃÖŖµćD![]() £¬Į¬½ÓBC£¬BD£¬CD£¬”ŃTµÄŌ²ŠÄĪŖT£Øt£¬©1£©£¬°ė¾¶ĪŖ1£¬ČōŌŚ”÷BCDÉĻ“ęŌŚŅ»µćN£¬Ź¹µćNŹĒ”ŃT”°ÓŃŗƵ攱£¬ĒóŌ²ŠÄTµÄŗį×ų±źtµÄȔֵ·¶Ī§£®
£¬Į¬½ÓBC£¬BD£¬CD£¬”ŃTµÄŌ²ŠÄĪŖT£Øt£¬©1£©£¬°ė¾¶ĪŖ1£¬ČōŌŚ”÷BCDÉĻ“ęŌŚŅ»µćN£¬Ź¹µćNŹĒ”ŃT”°ÓŃŗƵ攱£¬ĒóŌ²ŠÄTµÄŗį×ų±źtµÄȔֵ·¶Ī§£®
”¾“š°ø”æ£Ø1£©¢ŁB£»¢Ś0”Üm”Ü![]() £»£Ø2£©©4+3
£»£Ø2£©©4+3![]() ”Üt£¼3
”Üt£¼3![]()
”¾½āĪö”æ
£Ø1£©£©¢Łøł¾Ż”°ÓŃŗƵ攱µÄ¶ØŅ壬OB£½2r£½2£¬ĖłŅŌµćBŹĒ”ŃO”°ÓŃŗƵ攱£»
¢ŚÉčM£Øm£¬©![]() m+2 £©£¬øł¾Ż”°ÓŃŗƵ攱µÄ¶ØŅ壬OM£½
m+2 £©£¬øł¾Ż”°ÓŃŗƵ攱µÄ¶ØŅ壬OM£½![]()
![]() £¬½āµĆ0”Üm”Ü
£¬½āµĆ0”Üm”Ü![]() £»
£»
£Ø2£©B£Ø0£¬2£©£¬C£Ø3£¬3£©£¬D![]() £¬”ŃTµÄŌ²ŠÄĪŖT£Øt£¬©1£©£¬µćNŹĒ”ŃT”°ÓŃŗƵ攱£¬NT”Ü2r£½2£¬ĖłŅŌµćNÖ»ÄÜŌŚĻ߶ĪBDÉĻŌĖ¶Æ£¬¹żµćT×÷TN”ĶBDÓŚN£¬×÷TH”ĪyÖį£¬ÓėBD½»ÓŚµćH£®Ņ×ÖŖ”ĻBDO£½30”ć£¬”ĻOBD£½60”ć£¬NT£½
£¬”ŃTµÄŌ²ŠÄĪŖT£Øt£¬©1£©£¬µćNŹĒ”ŃT”°ÓŃŗƵ攱£¬NT”Ü2r£½2£¬ĖłŅŌµćNÖ»ÄÜŌŚĻ߶ĪBDÉĻŌĖ¶Æ£¬¹żµćT×÷TN”ĶBDÓŚN£¬×÷TH”ĪyÖį£¬ÓėBD½»ÓŚµćH£®Ņ×ÖŖ”ĻBDO£½30”ć£¬”ĻOBD£½60”ć£¬NT£½![]() HT£¬Ö±ĻßBD£ŗy£½©
HT£¬Ö±ĻßBD£ŗy£½©![]() x+2£¬H£Øt£¬©
x+2£¬H£Øt£¬©![]() t+2 ÉĻ£©£¬HT£½©
t+2 ÉĻ£©£¬HT£½©![]() t+2©£Ø©1£©£½©
t+2©£Ø©1£©£½©![]() t+3£¬NT£½
t+3£¬NT£½![]() HT£½
HT£½![]() £Ø©
£Ø©![]() t+3£©£½©
t+3£©£½©![]() t+
t+![]() £¬½ā³ötµÄ·¶Ī§£®
£¬½ā³ötµÄ·¶Ī§£®
½ā£ŗ£Ø1£©¢Ł”ßr£½1
”ąøł¾Ż”°ÓŃŗƵ攱µÄ¶ØŅ壬OB£½2r£½2
”ąµćBŹĒ”ŃO”°ÓŃŗƵ攱
OC£½3![]() >2r£¬²»ŹĒ”ŃO”°ÓŃŗƵ攱
>2r£¬²»ŹĒ”ŃO”°ÓŃŗƵ攱
A£Ø1£¬0£©ŌŚ”ŃOÉĻ£¬²»ŹĒ”ŃO”°ÓŃŗƵ攱
¹Ź“š°øĪŖB£»
¢ŚČēĶ¼£¬
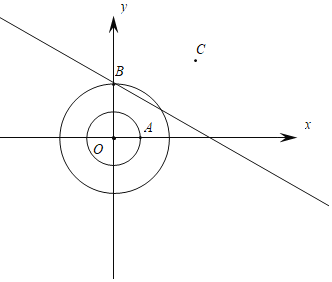
ÉčM£Øm£¬©![]() m+2 £©£¬øł¾Ż”°ÓŃŗƵ攱µÄ¶ØŅå
m+2 £©£¬øł¾Ż”°ÓŃŗƵ攱µÄ¶ØŅå
”ąOM£½![]()
ÕūĄķ£¬µĆ2m2©2![]() m”Ü0
mӆ0
½āµĆ0”Üm”Ü![]() £»
£»
”ąµćMµÄŗį×ų±źmµÄȔֵ·¶Ī§£ŗ0”Üm”Ü![]() £»
£»
£Ø2£©”ßB£Ø0,2£©,C£Ø3,3£©,D![]() ,”ŃTµÄŌ²ŠÄĪŖT£Øt,©1£©,µćNŹĒ”ŃT”°ÓŃŗƵ攱
,”ŃTµÄŌ²ŠÄĪŖT£Øt,©1£©,µćNŹĒ”ŃT”°ÓŃŗƵ攱
”ąNT”Ü2r£½2£¬
”ąµćNÖ»ÄÜŌŚĻ߶ĪBDÉĻŌĖ¶Æ£¬¹żµćT×÷TN”ĶBDÓŚN£¬×÷TH”ĪyÖį£¬ÓėBD½»ÓŚµćH£®
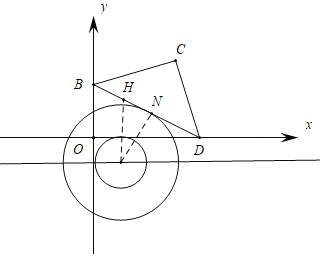
Ņ×ÖŖ”ĻBDO£½30”ć£¬
”ą”ĻOBD£½60”ć£¬
”ąNT£½![]() HT£¬
HT£¬
”ßB£Ø0£¬2£©£¬D![]() £¬
£¬
”ąÖ±ĻßBD£ŗy£½©![]() x+2£¬H£Øt£¬©
x+2£¬H£Øt£¬©![]() t+2 ÉĻ£©£¬
t+2 ÉĻ£©£¬
”ąHT£½©![]() t+2©£Ø©1£©£½©
t+2©£Ø©1£©£½©![]() t+3£¬
t+3£¬
”ąNT£½![]() HT£½
HT£½![]() £Ø©
£Ø©![]() t+3£©£½©
t+3£©£½©![]() t+
t+![]() £¬
£¬
”ą©![]() t+
t+![]() ”Ü2£¬
”Ü2£¬
”ąt”Ż©4+![]() £¬
£¬
µ±HÓėµćDÖŲŗĻŹ±£¬µćTµÄŗį×ų±źµČÓŚµćDµÄŗį×ų±ź£¬¼“t£½![]() £¬
£¬
“ĖŹ±µćN²»ŹĒ”°ÓŃŗƵ攱£¬
”ąt£¼![]() £¬
£¬
¹ŹŌ²ŠÄTµÄŗį×ų±źtµÄȔֵ·¶Ī§£ŗ©4+![]() ”Üt£¼
”Üt£¼![]() £®
£®


 ³õ֊ѧŅµæ¼ŹŌµ¼ÓėĮ·ĻµĮŠ“š°ø
³õ֊ѧŅµæ¼ŹŌµ¼ÓėĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øö²»ĶøĆ÷µÄ“ü×ÓĄļÓŠČōøÉøöŠ”Ēņ£¬ĖüĆĒ³żĮĖŃÕÉ«Ķā£¬ĘäĖü¶¼ĻąĶ¬£¬¼×Ķ¬Ń§“Ó“ü×ÓĄļĖ껜ƞ³öŅ»øöĒņ£¬¼ĒĻĀŃÕÉ«ŗó·Å»Ų“ü×ÓĄļ£¬Ņ”ŌČŗóŌŁ“ĪĖ껜ƞ³öŅ»øöĒņ£¬¼ĒĻĀŃÕÉ«£¬”£¬¼×Ķ¬Ń§·“ø““óĮæŹµŃéŗó£¬øł¾Ż°×Ēņ³öĻÖµÄʵĀŹ»ęÖĘĮĖČēĶ¼ĖłŹ¾µÄĶ³¼ĘĶ¼£¬ŌņĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£Ø””””£©
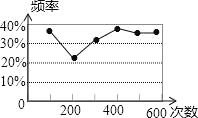
A. “ü×ÓŅ»¶ØÓŠČżøö°×Ēņ
B. “ü×ÓÖŠ°×ĒņÕ¼Š”Ēņ×ÜŹżµÄŹ®·Ö֮ȿ
C. ŌŁĆžČż“ĪĒņ£¬Ņ»¶ØÓŠŅ»“ĪŹĒ°×Ēņ
D. ŌŁĆž1000“Ī£¬Ćž³ö°×ĒņµÄ“ĪŹż»į½Ó½ü330“Ī
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
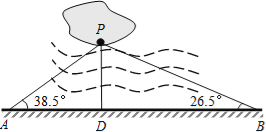
”¾ĢāÄæ”æČēĶ¼£¬ŅęŃōŹŠč÷ɽŗžÖŠÓŠŅ»¹ĀĮ¢Š”µŗ£¬ŗž±ßÓŠŅ»Ģõ±ŹÖ±µÄ¹Ū¹āŠ”µĄAB£¬ĻÖ¾ö¶Ø“ÓŠ”µŗ¼ÜŅ»×łÓė¹Ū¹āŠ”µĄ“¹Ö±µÄŠ”ĒÅPD£¬Š”ÕÅŌŚŠ”µĄÉĻ²āµĆČēĻĀŹż¾Ż£ŗAB=80.0Ć×£¬”ĻPAB=38.5”ć£¬”ĻPBA=26.5£®Ēė°ļÖśŠ”ÕÅĒó³öŠ”ĒÅPDµÄ³¤²¢Č·¶ØŠ”ĒÅŌŚŠ”µĄÉĻµÄĪ»ÖĆ£®£ØŅŌA£¬BĪŖ²ĪÕÕµć£¬½į¹ū¾«Č·µ½0.1Ć×£©
£Ø²Īæ¼Źż¾Ż£ŗsin38.5”ć=0.62£¬cos38.5”ć=0.78£¬tan38.5”ć=0.80£¬sin26.5”ć=0.45£¬cos26.5”ć=0.89£¬tan26.5”ć=0.50£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬AB£¾AD£¬”ĻA£½60”ć£¬
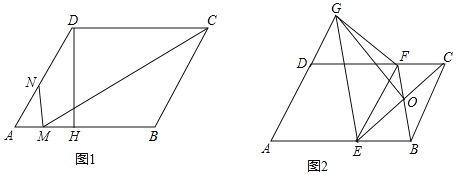
£Ø1£©ČēĶ¼1£¬¹żµćD×÷DH”ĶABÓŚµćH£¬MCĘ½·Ö”ĻDCB½»AB±ßÓŚµćM£¬¹żM×÷MN”ĶAB½»AD±ßÓŚµćN£¬AN£ŗND£½2£ŗ3£¬Ę½ŠŠĖıߊĪABCDµÄĆ껿ĪŖ60![]() £¬ĒóMNµÄ³¤¶Č£®
£¬ĒóMNµÄ³¤¶Č£®
£Ø2£©ČēĶ¼2£¬E”¢F·Ö±šĪŖ±ßAB”¢CDÉĻŅ»µć£¬ĒŅAE£½AD£½DF£¬Į¬½ÓBF”¢EC½»ÓŚµćO£¬GĪŖADŃÓ³¤ĻßÉĻŅ»µć£¬Į¬½ÓGE”¢GFŗĶGO£¬Čō”ĻGFD£½”ĻEFB£¬ĒóÖ¤£ŗGO”ĶEC£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ±ß³¤ĪŖ1µÄŠ”Õż·½ŠĪ×é³ÉµÄĶųøńÖŠ£¬”÷ABCµÄČżøö¶„µć¾łŌŚøńµćÉĻ£®½«”÷ABCČʵćAĖ³Ź±ÕėŠż×Ŗ90”ćµĆµ½”÷AB1C1£®
£Ø1£©ŌŚĶųøńÖŠ»³ö”÷AB1C1£»
£Ø2£©¼ĘĖćµćBŠż×Ŗµ½B1µÄ¹ż³ĢÖŠĖł¾¹żµÄĀ·¾¶³¤£®£Ø½į¹ū±£Įō¦Š£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£¬»Ų“šĪŹĢā.
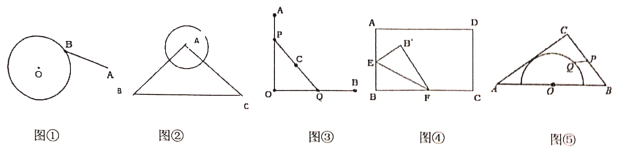
²ÄĮĻ£ŗĒóŌ²ĶāŅ»¶Øµćµ½Ō²ÉĻ¾ąĄė×īŠ”ÖµŹĒ°²»ÕŹ”ÖŠæ¼ŹżŃ§½ĻĪŖ³£¼ūµÄŅ»ÖÖĢāŠĶ£¬“ĖĄąĢāŠĶŹŌĢāÓŠŹ±³öĢāÕß½«Ō²Ņž²Ų£¬¹ŹÓÖ³ĘĪŖ”°ŅžŌ²ĪŹĢā”±.½ā¾öÕāĄąĪŹĢā£¬¹Ų¼üŹĒŅŖÕŅµ½¶ÆµćµÄŌĖ¶Æ¹ģ¼££¬¼“øĆ¶ÆµćŹĒČĘÄÄŅ»øö¶ØµćŠż×Ŗ£¬ĒŅÄܱ£³ÖŠż×Ŗ°ė¾¶²»±ä.“Ó¶ųÕŅµ½¶ÆµćĖłŌŚµÄŅž²ŲŌ²£¬½ųĆę×Ŗ»»³ÉŌ²ĶāŅ»µćµ½Ō²ŠÄµÄ¾ąĄė¼õ°ė¾¶£¬ĒóµĆ×īŠ”Öµ.
½ā¾öĪŹĢā£ŗ
£Ø1£©ČēĶ¼¢Ł£¬Ō²OµÄ°ė¾¶ĪŖ1£¬Ō²ĶāŅ»µćAµ½Ō²ŠÄµÄ¾ąĄėĪŖ3£¬Ō²ÉĻŅ»¶ÆµćB£¬µ±A”¢O”¢BĀś×ćĢõ¼ž____________Ź±£¬![]() ÓŠ×īŠ”ÖµĪŖ____________.
ÓŠ×īŠ”ÖµĪŖ____________.
£Ø2£©ČēĶ¼¢Ś£¬µČŃü![]() Į½Ńü³¤ĪŖ5£¬µ×±ß³¤ĪŖ6£¬ŅŌAĪŖŌ²ŠÄ£¬2ĪŖ°ė¾¶×÷Ō²£¬Ō²ÉĻ¶ÆµćPµ½
Į½Ńü³¤ĪŖ5£¬µ×±ß³¤ĪŖ6£¬ŅŌAĪŖŌ²ŠÄ£¬2ĪŖ°ė¾¶×÷Ō²£¬Ō²ÉĻ¶ÆµćPµ½![]() µÄ¾ąĄė×īŠ”ÖµĪŖ__________.
µÄ¾ąĄė×īŠ”ÖµĪŖ__________.
£Ø3£©ČēĶ¼¢Ū£¬![]() £¬P”¢Q·Ö±šŹĒÉäĻß
£¬P”¢Q·Ö±šŹĒÉäĻß![]() ”¢
”¢![]() ÉĻĮ½øö¶Æµć£¬CŹĒĻ߶Ī
ÉĻĮ½øö¶Æµć£¬CŹĒĻ߶Ī![]() µÄÖŠµć£¬ĒŅ
µÄÖŠµć£¬ĒŅ![]() £¬ŌņŌŚĻ߶Ī
£¬ŌņŌŚĻ߶Ī![]() »¬¶ÆµÄ¹ż³ĢÖŠ£¬ĒóµćCŌĖ¶ÆŠĪ³ÉµÄĀ·¾¶³¤£¬²¢ĖµĆ÷ĄķÓÉ.
»¬¶ÆµÄ¹ż³ĢÖŠ£¬ĒóµćCŌĖ¶ÆŠĪ³ÉµÄĀ·¾¶³¤£¬²¢ĖµĆ÷ĄķÓÉ.
£Ø4£©ČēĶ¼¢Ü£¬ŌŚ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬µćEŹĒ
£¬µćEŹĒ![]() ÖŠµć£¬µćFŹĒ
ÖŠµć£¬µćFŹĒ![]() ÉĻŅ»µć£¬°Ń
ÉĻŅ»µć£¬°Ń![]() ŃŲ×Å
ŃŲ×Å![]() ·ÕŪ£¬µćBĀäŌŚµć
·ÕŪ£¬µćBĀäŌŚµć![]() “¦£¬Ēó
“¦£¬Ēó![]() µÄ×īŠ”Öµ£¬²¢ĖµĆ÷ĄķÓÉ.
µÄ×īŠ”Öµ£¬²¢ĖµĆ÷ĄķÓÉ.
£Ø5£©ČēĶ¼¢Ż£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬ŅŌ±ß
£¬ŅŌ±ß![]() ÖŠµćOĪŖŌ²ŠÄ£¬×÷°ėŌ²Óė
ÖŠµćOĪŖŌ²ŠÄ£¬×÷°ėŌ²Óė![]() ĻąĒŠ£¬µćP£¬Q·Ö±šŹĒ±ß
ĻąĒŠ£¬µćP£¬Q·Ö±šŹĒ±ß![]() ŗĶ°ėŌ²ÉĻµÄ¶Æµć£¬Į¬½Ó
ŗĶ°ėŌ²ÉĻµÄ¶Æµć£¬Į¬½Ó![]() £¬Ēó
£¬Ēó![]() ³¤µÄ×īŠ”Öµ£¬²¢ĖµĆ÷ĄķÓÉ.
³¤µÄ×īŠ”Öµ£¬²¢ĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÓĪĄÖŌ°ÓŠŅ»øöÖ±¾¶ĪŖ16Ć×µÄŌ²ŠĪÅēĖ®³Ų£¬ÅēĖ®³ŲµÄÖܱßÓŠŅ»Č¦ÅēĖ®Ķ·£¬Åē³öµÄĖ®ÖłĪŖÅ×ĪļĻߣ¬ŌŚ¾ąĖ®³ŲÖŠŠÄ3Ćד¦“ļµ½×īøߣ¬ø߶ČĪŖ5Ć×£¬ĒŅø÷·½ĻņÅē³öµÄĖ®ÖłĒ”ŗĆŌŚÅēĖ®³ŲÖŠŠÄµÄ×°ŹĪĪļ“¦»ŲŗĻ£¬ČēĶ¼ĖłŹ¾£¬ŅŌĖ®Ę½·½ĻņĪŖ![]() Öį£¬ÅēĖ®³ŲÖŠŠÄĪŖŌµć½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ.
Öį£¬ÅēĖ®³ŲÖŠŠÄĪŖŌµć½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ.
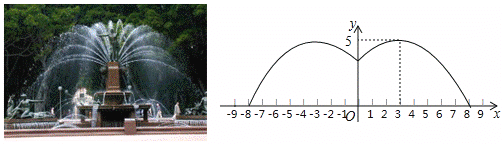
£Ø1£©ĒóĖ®ÖłĖłŌŚÅ×ĪļĻߣصŚŅ»ĻóĻŽ²æ·Ö£©µÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ĶõŹ¦øµŌŚÅēĖ®³ŲÄŚĪ¬ŠŽÉč±øĘŚ¼ä£¬ÅēĖ®¹ÜŅāĶāÅēĖ®£¬ĪŖĮĖ²»±»ĮÜŹŖ£¬Éķøß1.8Ć×µÄĶõŹ¦øµÕ¾Į¢Ź±±ŲŠėŌŚĄėĖ®³ŲÖŠŠÄ¶ąÉŁĆ×ŅŌÄŚ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µć![]() ·Ö±šŌŚÕżČż½ĒŠĪ
·Ö±šŌŚÕżČż½ĒŠĪ![]() µÄČż±ßÉĻ£¬ĒŅ
µÄČż±ßÉĻ£¬ĒŅ![]() Ņ²ŹĒÕżČż½ĒŠĪ.Čō
Ņ²ŹĒÕżČż½ĒŠĪ.Čō![]() µÄ±ß³¤ĪŖ
µÄ±ß³¤ĪŖ![]() £¬
£¬![]() µÄ±ß³¤ĪŖ
µÄ±ß³¤ĪŖ![]() £¬Ōņ
£¬Ōņ![]() µÄÄŚĒŠŌ²°ė¾¶ĪŖ__________£®
µÄÄŚĒŠŌ²°ė¾¶ĪŖ__________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÓŠŅ»×łÅ×ĪļĻߊĪ¹°ĒÅ£¬ŌŚÕż³£Ė®Ī»Ź±Ė®ĆęABµÄæķĪŖ20Ć×£¬Čē¹ūĖ®Ī»ÉĻÉż3Ć×£¬ŌņĖ®ĆęCDµÄæķŹĒ10Ć×£®
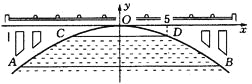
£Ø1£©½ØĮ¢ČēĶ¼ĖłŹ¾µÄÖ±½Ē×ų±źĻµ£¬Ēó“ĖÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µ±Ė®Ī»ŌŚÕż³£Ė®Ī»Ź±£¬ÓŠŅ»ĖŅæķĪŖ6Ć׵Ļõ“¬¾¹żÕāĄļ£¬“¬²ÕÉĻÓŠøß³öĖ®Ćę3.6Ć׵ij¤·½Ģå»õĪļ£Ø»õĪļÓė»õ“¬Ķ¬æķ£©£®ĪŹ£ŗ“Ė“¬ÄÜ·ńĖ³ĄūĶعżÕā׳¹°ĒÅ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com