
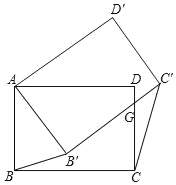
【题目】如图,将矩形ABCD绕点A按逆时针方向旋转一定角度后,BC的对应边B′C交CD边于点G,如果当AB′=B′G时量得AD=7,CG=4,连接BB′、CC′,那么![]() =_____.
=_____.
【答案】![]()
【解析】
先连接AC,AG,AC',构造直角三角形以及相似三角形,根据△ABB'∽△ACC',可得到![]() ,设AB=AB'=x,则AG=
,设AB=AB'=x,则AG=![]() x,DG=x-4,Rt△ADG中,根据勾股定理可得方程72+(x-4)2=(
x,DG=x-4,Rt△ADG中,根据勾股定理可得方程72+(x-4)2=(![]() x)2,求得AB的长以及AC的长,即可得到所求的比值.
x)2,求得AB的长以及AC的长,即可得到所求的比值.
解:如图,连接AC,AG,AC',
由旋转可得,AB=AB',AC=AC',∠BAB'=∠CAC',
∴![]() ,
,
∴△ABB'∽△ACC',
∴![]() ,
,
∵AB'=B'G,∠AB'G=∠ABC=90°,
∴△AB'G是等腰直角三角形,
∴AG=![]() AB',
AB',
设AB=AB'=x,则AG=![]() x,DG=x﹣4,
x,DG=x﹣4,
∵Rt△ADG中,AD2+DG2=AG2,
∴72+(x﹣4)2=(![]() x)2,
x)2,
解得x1=5,x2=﹣13(舍去),
∴AB=5,
∴Rt△ABC中,AC=![]() ,
,
∴![]() ,
,
故答案为:![]() .
.



科目:初中数学 来源: 题型:
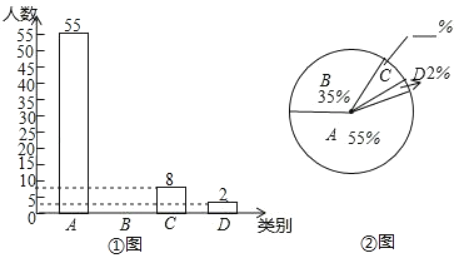
【题目】我省某地区为了了解2017年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读重点高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如①图,如②图)
(1)该地区共调查了_____名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2017年初中毕业生共有4000人,请估计该地区今年初中毕业生中读重点高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极配合我市文明城市创建,居委会组织了两个检查组,分别对辖区内新华园、清华园、德才园、御花园四个小区“垃圾分类”和“违规停车”的情况进行抽查,每个检查组随机抽取辖区内的一个小区进行检查.
(1)“违规停车”检查组抽到新华园小区的概率为_____;
(2)求两个组恰好同时抽到御花园小区进行检查的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
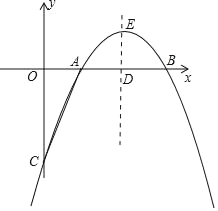
【题目】如图所示,已知抛物线y=﹣x2+bx+c与x轴相交于A、B两点,且点A的坐标为(1,0),与y轴交于点C,对称轴直线x=2与x轴相交于点D,点P是抛物线对称轴上的一个动点,以每秒1个单位长度的速度从抛物线的顶点E向下运动,设点P运动的时间为t(s).
(1)点B的坐标为 ,抛物线的解析式是 ;
(2)求当t为何值时,△PAC的周长最小?
(3)当t为何值时,△PAC是以AC为腰的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行“校园朗读者”朗诵大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
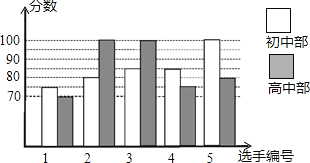
(1)根据图示填写表格;
平均分(分) | 中位数(分) | 众数(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
(2)结合两队成绩的平均数和中位数, 队的决赛成绩较好;
(3)已知高中代表队决赛成绩的方差为160,计算初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.(方差公式:S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2]
)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
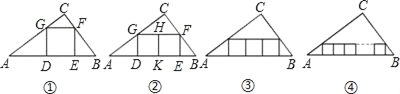
【题目】猜想归纳:为了建设经济型节约型社会,“先锋”材料厂把一批三角形废料重新利用,因此工人师傅需要把它们截成不同大小的正方形铁片.(已知:AC=40,BC=30,∠C=90°)
(1)如图①,若截取△ABC的内接正方形DEFG,请你求出此正方形的边长;
(2)如图②,若在△ABC内并排截取两个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(3)如图③,若在△ABC内并排截取三个相同的正方形(它们组成的矩形内接于△ABC),请你求此正方形的边长;
(4)猜想:如图④,假设在△ABC内并排截取n个相同的正方形,使它们组成的矩形内接于△ABC,则此正方形的边长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4张相同的卡片上分别写有数字1、2、3、4,将卡片背面朝上,洗匀后从中任意抽取1张,将卡片上的数字作为被减数;一只不透明的袋子中装有标号为1、2、3的3个小球,这些球除标号外都相同,搅匀后从中任意摸出1个球,将摸到的球的标号作为减数.
(1)求这两个数的差为0的概率;
(2)游戏规则规定:当抽到的这两个数的差为非负数时,甲获胜;否则,乙获胜.这样的规则公平吗?如果不公平,请设计一个公平的规则,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com