
【题目】如图,菱形ABCD的对角线交于O点,DE∥AC,CE∥BD,
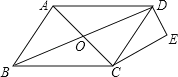
(1)求证:四边形OCED是矩形;
(2)若AD=5,BD=8,计算sin∠DCE的值.
【答案】(1)见解析;(2)sin∠DCE=![]() .
.
【解析】
试题(1)首先证明四边形OCED是平行四边形,再根据菱形的性质可得AC⊥BD,进而得到四边形OCED是矩形;
(2)首先根据菱形的性质可得![]() =4,OC=OA,AD=CD,然后再根据勾股定理可计算出DE=OC=3,再利用三角函数定义可得答案.
=4,OC=OA,AD=CD,然后再根据勾股定理可计算出DE=OC=3,再利用三角函数定义可得答案.
(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴四边形OCED是矩形;
(2)解:∵四边形ABCD是菱形,BD=8,
∴![]() =4,OC=OA,AD=CD,
=4,OC=OA,AD=CD,
∵AD=5,
∴OC=![]() =3,
=3,
∵四边形OCED是矩形,
∴DE=OC=3,
在Rt△DEC中,sin∠DCE=![]() .
.


科目:初中数学 来源: 题型:
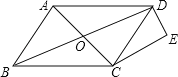
【题目】如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F
(1)求证:△ADE∽△BEF;
(2)设H是ED上一点,以EH为直径作⊙O,DF与⊙O相切于点G,若DH=OH=3,求图中阴影部分的面积(结果保留到小数点后面第一位,![]() ≈1.73,π≈3.14).
≈1.73,π≈3.14).
查看答案和解析>>
科目:初中数学 来源: 题型:
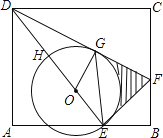
【题目】如图,图①所示是一个长为2m,宽为2n的长方形,用剪刀均分成四个小长方形,然后按图②的方式拼成一个大正方形.
(1)图②中的大正方形的边长等于 ,图②中的小正方形的边长等于 ;
(2)图②中的大正方形的面积等于 ,图②中的小正方形的面积等于 ;图①中每个小长方形的面积是 ;
(3)观察图②,你能写出(m+n)2,(m﹣n)2,mn这三个代数式间的等量关系吗? .
查看答案和解析>>
科目:初中数学 来源: 题型:
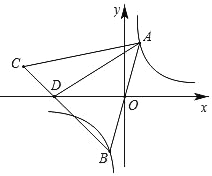
【题目】如图,已知点A是反比例函数y=![]() 的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为__.
的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
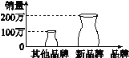
【题目】2018年某新品牌牛奶公司为了宣传其公司牛奶的销售量大,把该品牌牛奶的销售量与其他品牌牛奶的销售量对比绘制了如图K-28-3所示的广告,并形象地用牛奶瓶代替条形图,从销售量来看,新品牌牛奶的销售量是其他品牌牛奶的2倍.请分析这个图合理吗.
答:________,理由是______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求证:该抛物线与x轴总有交点;
(2)若该抛物线与x轴有一个交点的横坐标大于3且小于5,求m的取值范围;
(3)设抛物线![]() 与
与![]() 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线![]() 的对称点恰好是点M,求
的对称点恰好是点M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在线BC、CD上运动,且满足∠EAF=45°,AE、AF分别与BD相交于点M、N.下列说法中:①BE+DF=EF;②点A到线段EF的距离一定等于正方形的边长;③若tan∠BAE=![]() ,则tan∠DAF=
,则tan∠DAF=![]() ;④若BE=2,DF=3,则S△AEF=18.其中结论正确的是__(将正确的序号写在横线上)
;④若BE=2,DF=3,则S△AEF=18.其中结论正确的是__(将正确的序号写在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
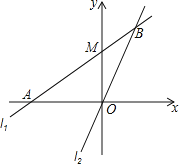
【题目】如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,6)
(1)求直线l1的表达式
(2)直线l1与y轴交于点M,求△BOM的面积;
(3)过动点P(m,0)且垂于x轴的直线与l1,l2的交点分别为C,D,当点C位于点D下方时,写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com