
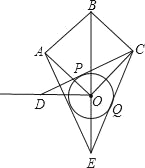
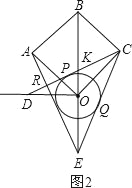
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкБпГЄЮЊ4![]() е§ЗНаЮOABCжаЃЌOBЮЊЖдНЧЯпЃЌЙ§ЕуOзїOBЕФДЙЯпЃЎвдЕуOЮЊдВаФЃЌrЮЊАыОЖзїдВЃЌЙ§ЕуCзіЁбOЕФСНЬѕЧаЯпЗжБ№НЛOBДЙЯпЁЂBOбгГЄЯпгкЕуDЁЂEЃЌCDЁЂCEЗжБ№ЧаЁбOгкЕуPЁЂQЃЌСЌНгAEЃЎ
е§ЗНаЮOABCжаЃЌOBЮЊЖдНЧЯпЃЌЙ§ЕуOзїOBЕФДЙЯпЃЎвдЕуOЮЊдВаФЃЌrЮЊАыОЖзїдВЃЌЙ§ЕуCзіЁбOЕФСНЬѕЧаЯпЗжБ№НЛOBДЙЯпЁЂBOбгГЄЯпгкЕуDЁЂEЃЌCDЁЂCEЗжБ№ЧаЁбOгкЕуPЁЂQЃЌСЌНгAEЃЎ
ЃЈ1ЃЉЧыЯШдквЛИіЕШбќжБНЧШ§НЧаЮФкЬНОПtan22.5ЁуЕФжЕЃЛ
ЃЈ2ЃЉЧѓжЄЃК
ЂйDOЃНOEЃЛ
ЂкAEЃНCDЃЌЧвAEЁЭCDЃЎ
ЃЈ3ЃЉЕБOAЃНODЪБЃК
ЂйЧѓЁЯAECЕФЖШЪ§ЃЛ
ЂкЧѓrЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉtan22.5ЁуЃН![]() Љ1ЃЛЃЈ2ЃЉЂйМћНтЮіЃЛЂкМћНтЮіЃЛЃЈ3ЃЉЂйЁЯAECЕФЖШЪ§ЮЊ45ЁуЃЛЂкr=2
Љ1ЃЛЃЈ2ЃЉЂйМћНтЮіЃЛЂкМћНтЮіЃЛЃЈ3ЃЉЂйЁЯAECЕФЖШЪ§ЮЊ45ЁуЃЛЂкr=2![]()
ЁОНтЮіЁП
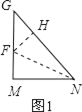
ЃЈ1ЃЉШчЭМ1ЃЌЁїGMNЪЧЕШбќжБНЧШ§НЧаЮЃЌЙ§ЕуNзїNFЦНЗжЁЯMNGЃЌНЛGMгкЕуFЃЌЙ§ЕуFзїFHЁЭNGгкHЃЎИљОнНЧЦНЗжЯпЕФаджЪПЩЕУFMЃНFHЃЌРћгУШ§НЧКЏЪ§ПЩЕУGFЃН![]() FHЃЌДгЖјгаGFЃН
FHЃЌДгЖјгаGFЃН![]() FMЃЌНјЖјПЩЕУMNЃНЃЈ
FMЃЌНјЖјПЩЕУMNЃНЃЈ![]() +1ЃЉFMЃЌдкRtЁїFMNжадЫгУШ§НЧКЏЪ§ОЭПЩЧѓГіtan22.5ЁуЕФжЕЃЎ
+1ЃЉFMЃЌдкRtЁїFMNжадЫгУШ§НЧКЏЪ§ОЭПЩЧѓГіtan22.5ЁуЕФжЕЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЂйвзжЄЁЯDOCЃНЁЯEOCЃН135ЁуЃЌИљОнЧаЯпГЄЖЈРэПЩЕУЁЯPCOЃНЁЯQCOЃЌДгЖјПЩжЄЕНЁїDOCЁеЁїEOCЃЌдђгаODЃНOEЃЎЂквзжЄЁїAOEЁеЁїCODЃЌДгЖјгаAEЃНCDЃЌЁЯAEOЃНЁЯCDOЃЎгЩЁЯKDO+ЁЯDKOЃН90ЁуПЩЕУЁЯAEO+ЁЯDKOЃН90ЁуЃЌМДПЩжЄЕНAEЁЭCDЃЎ
ЃЈ3ЃЉСЌНгOQЃЌШчЭМ3ЃЎгЩOCЃНOEЕУЁЯOECЃНЁЯOCEЃЌДгЖјЧѓГіЁЯOECЃН22.5ЁуЃЎдкRtЁїOQEжаЃЌдЫгУШ§НЧКЏЪ§ПЩЕУЕН![]() ШЛКѓдЫгУЙДЙЩЖЈРэОЭПЩЧѓГіrЕФжЕЃЎ
ШЛКѓдЫгУЙДЙЩЖЈРэОЭПЩЧѓГіrЕФжЕЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЁїGMNЪЧЕШбќжБНЧШ§НЧаЮЃЎ
дђгаЁЯMЃН90ЁуМДGMЁЭMNЃЌMGЃНMNЃЌЁЯMGNЃНЁЯMNGЃН45ЁуЃЎ
Й§ЕуNзїNFЦНЗжЁЯMNGЃЌНЛGMгкЕуFЃЌЙ§ЕуFзїFHЁЭNGгкHЃЎ
ЁпNFЦНЗжЁЯMNGЃЌFHЁЭNGЃЌFMЁЭMNЃЌ
Ёр![]()
ЁпFHЁЭNGМДЁЯFHGЃН90ЁуЃЌЁЯGЃН45ЁуЃЌ
Ёр![]()
ЁрGFЃН![]() FHЃЎ
FHЃЎ
ЁрGFЃН![]() FMЃЎ
FMЃЎ
ЁрMNЃНMGЃНMF+FGЃНMF+![]() FMЃНЃЈ
FMЃНЃЈ![]() +1ЃЉFMЃЎ
+1ЃЉFMЃЎ
дкRtЁїFMNжаЃЌ
tanЁЯFNMЃНtan22.5Ёу![]()
Ёрtan22.5ЁуЃН![]() Љ1ЃЎ
Љ1ЃЎ
ЃЈ2ЃЉЂйШчЭМ2ЃЌ
ЁпЫФБпаЮOABCЪЧе§ЗНаЮЃЌ
ЁрOAЃНOCЃЌЁЯAOBЃНЁЯBOCЃН45ЁуЃЎ
ЁрЁЯEOCЃН180ЁуЉЁЯBOCЃН135ЁуЃЎ
ЁпODЁЭOBМДЁЯDOBЃН90ЁуЃЌ
ЁрЁЯDOCЃНЁЯDOB+ЁЯBOCЃН135ЁуЃЎ
ЁрЁЯDOCЃНЁЯEOCЃЎ
ЁпCDЁЂCEЗжБ№гыЁбOЯрЧагкPЁЂQЃЌ
ЁрЁЯPCOЃНЁЯQCOЃЎ
дкЁїDOCКЭЁїEOCжаЃЌ
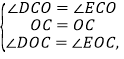
ЁрЁїDOCЁеЁїEOCЃЈASAЃЉЃЎ
ЁрODЃНOEЃЎ
ЂкЁпЁЯAOBЃН45ЁуЃЌ
ЁрЁЯAOEЃН135ЁуЃЎ
ЁрЁЯAOEЃНЁЯDOCЃЎ
дкЁїAOEКЭЁїCODжаЃЌ
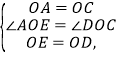
ЁрЁїAOEЁеЁїCODЃЈSASЃЉЃЎ
ЁрAEЃНCDЃЌЁЯAEOЃНЁЯCDOЃЎ
ЁпЁЯDOBЃН90ЁуЃЌЁрЁЯKDO+ЁЯDKOЃН90ЁуЃЎ
ЁрЁЯAEO+ЁЯDKOЃН90ЁуЃЎ
ЁрЁЯKREЃН90ЁуЃЎ
ЁрAEЁЭCDЃЎ
ЃЈ3ЃЉЂйЁпOAЃНODЃЌOAЃНOCЃЌODЃНOEЃЌ
ЁрOAЃНODЃНOEЃНOCЃЎ
ЁрЕуAЁЂDЁЂEЁЂCдквдЕуOЮЊдВаФЃЌOAЮЊАыОЖЕФдВЩЯЃЎ
ЁрИљОндВжмНЧЖЈРэПЩЕУЁЯAECЃН![]() ЁЯAOCЃН45ЁуЃЎ
ЁЯAOCЃН45ЁуЃЎ
ЁрЁЯAECЕФЖШЪ§ЮЊ45ЁуЃЎ
ЂкСЌНгOQЃЌШчЭМ3ЃЎ
ЁпOCЃНOEЃЌЁрЁЯOECЃНЁЯOCEЃЎ
ЁпЁЯBOCЃНЁЯOEC+ЁЯOCEЃН2ЁЯOECЃН45ЁуЃЌ
ЁрЁЯOECЃН22.5Ёу
ЁпCEгыЁбOЯрЧагкЕуQЃЌ
ЁрOQЁЭECЃЌМДЁЯOQEЃН90ЁуЃЎ
дкRtЁїOQEжаЃЌ
ЁпЁЯOQEЃН90ЁуЃЌ
ЁрtanЁЯOEQЃНtan22.5Ёу![]()
ЁпOQЃНrЃЌ
Ёр![]()
ЁпЁЯOQEЃН90ЁуЃЌ
ЁрOQ2+QE2ЃНOE2ЃЎ
Ёп![]()
Ёр![]()
ећРэЕУ![]()
НтЕУЃКrЃН![]() ЃЎ
ЃЎ
ЁрrЕФжЕЮЊ![]() ЃЎ
ЃЎ
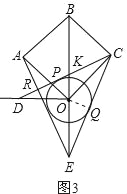


 жЧЛлаЁИДЯАЯЕСаД№АИ
жЧЛлаЁИДЯАЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2018ФъЮвЪаЕФЦъГШЯВЛёЗсЪеЃЌЦъГШвЛЩЯЪаЃЌЫЎЙћЕъЕФГТРЯАхгУ2400дЊЙКНјвЛХњЦъГШЃЌКмПьЪлЭъЃЛГТРЯАхгжгУ6000дЊЙКНјЕкЖўХњЦъГШЃЌЫљЙКМўЪ§ЪЧЕквЛХњЕФ2БЖЃЌЕЋНјМлБШЕквЛХњУПМўЖрСЫ20дЊЃЎ
ЃЈ1ЃЉЕквЛХњЦъГШУПМўНјМлЖрЩйдЊЃП
ЃЈ2ЃЉГТРЯАхвдУПМў120дЊЕФМлИёЯњЪлЕкЖўХњЦъГШЃЌЪлГі60%КѓЃЌЮЊСЫОЁПьЪлЭъЃЌОіЖЈДђелДйЯњЃЌвЊЪЙЕкЖўХњЦъГШЕФЯњЪлзмРћШѓВЛЩйгк480дЊЃЌЪЃгрЕФЦъГШУПМўЪлМлзюЕЭДђМИелЃПЃЈРћШѓЃНЪлМлЉНјМлЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧвЛИіЧуаБНЧЮЊ ЕФаБЦТЃЌНЋвЛИіаЁЧђДгаБЦТЕФЦТНХ O ЕуДІХзГіЃЌТфдк AЕуДІЃЌаЁЧђЕФдЫЖЏТЗЯпПЩвдгУХзЮяЯп![]() РДПЬЛЃЌвбжЊ tan
РДПЬЛЃЌвбжЊ tan ![]()
ЃЈ1ЃЉЧѓХзЮяЯпБэДяЪНМАЕу A ЕФзјБъ.
ЃЈ2ЃЉЧѓаЁЧђдкдЫЖЏЙ§ГЬжаРыаБЦТЦТУц OA ЕФзюДѓОрРы.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
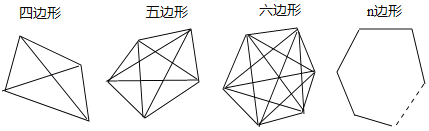
ЁОЬтФПЁПСЌНгЖрБпаЮШЮвтСНИіВЛЯрСкЖЅЕуЕФЯпЖЮГЦЮЊЖрБпаЮЕФЖдНЧЯпЃЎ
ЃЈ1ЃЉЫФЁЂЮхЁЂСљЁЂnБпаЮЖдНЧЯпЬѕЪ§ЗжБ№ЮЊ ЁЂ ЁЂ ЁЂ ЃЎ
ЃЈ2ЃЉЖрБпаЮПЩвдга12ЬѕЖдНЧЯпТ№ЃПШчЙћПЩвдЃЌЧѓЖрБпаЮЕФБпЪ§ЃЛШчЙћВЛПЩвдЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєвЛИіnБпаЮЕФФкНЧКЭЮЊ1800ЁуЃЌЧѓЫќЖдНЧЯпЕФЬѕЪ§ЃЎ
ЃЈ4ЃЉвбжЊk-1БпаЮЕФЖдНЧЯпЬѕЪ§ЪЧ![]() ,Чѓk+1БпаЮЕФЖдНЧЯпЬѕЪ§ЃЈk>4ЃЉЃЎ
,Чѓk+1БпаЮЕФЖдНЧЯпЬѕЪ§ЃЈk>4ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЃКШчЭМЃЈ1ЃЉЃЌЕуEЁЂFЗжБ№дке§ЗНаЮABCDЕФБпBCЁЂCDЩЯЃЌЁЯEAF=45ЁуЃЌЪдХаЖЯBEЁЂEFЁЂFDжЎМфЕФЪ§СПЙиЯЕЃЎ
ЁОЗЂЯжжЄУїЁПаЁДЯАбЁїABEШЦЕуAФцЪБеыа§зЊ90ЁужСЁїADGЃЌДгЖјЗЂЯжEF=BE+FDЃЌЧыФуРћгУЭМЃЈ1ЃЉжЄУїЩЯЪіНсТлЃЎ
ЁОРрБШв§ЩъЁПШчЭМЃЈ2ЃЉЃЌЫФБпаЮABCDжаЃЌЁЯBADЁй90ЁуЃЌAB=ADЃЌЁЯB+ЁЯD=180ЁуЃЌЕуEЁЂFЗжБ№дкБпBCЁЂCDЩЯЃЌдђЕБЁЯEAFгыЁЯBADТњзуЁЁ ЙиЯЕЪБЃЌШдгаEF=BE+FDЃЛЧыжЄУїФуЕФНсТл.

ЁОЬНОПгІгУЁПШчЭМЃЈ3ЃЉЃЌдкФГЙЋдАЕФЭЌвЛЫЎЦНУцЩЯЃЌЫФЬѕЭЈЕРЮЇГЩЫФБпаЮABCDЃЎвбжЊAB=AD=80УзЃЌЁЯB=60ЁуЃЌЁЯADC=120ЁуЃЌЁЯBAD=150ЁуЃЌЕРТЗBCЁЂCDЩЯЗжБ№гаОАЕуEЁЂFЃЌЧвAEЁЭADЃЌDF=40ЃЈ![]() Љ1ЃЉУзЃЌЯжвЊдкEЁЂFжЎМфаовЛЬѕБЪжБЕРТЗЃЌЧѓетЬѕЕРТЗEFЕФГЄ.ЃЈНсЙћШЁећЪ§ЃЌВЮПМЪ§ОнЃК
Љ1ЃЉУзЃЌЯжвЊдкEЁЂFжЎМфаовЛЬѕБЪжБЕРТЗЃЌЧѓетЬѕЕРТЗEFЕФГЄ.ЃЈНсЙћШЁећЪ§ЃЌВЮПМЪ§ОнЃК ![]() =1.41ЃЌ
=1.41ЃЌ ![]() =1.73ЃЉ
=1.73ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
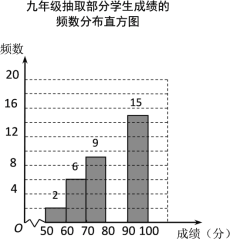
ЁОЬтФПЁПФГаЃзщжЏОХФъМЖбЇЩњВЮМгККзжЬ§аДДѓШќЃЌВЂЫцЛњГщШЁВПЗжбЇЩњГЩМЈзїЮЊбљБОНјааЗжЮіЃЌЛцжЦГЩШчЯТЕФЭГМЦБэЃК
![]()
ГЩМЈx/Зж | ЦЕЪ§ | ЦЕТЪ | |
Ек1ЖЮ | xЃМ60 | 2 | 0.04 |
Ек2ЖЮ | 60ЁмxЃМ70 | 6 | 0.12 |
Ек3ЖЮ | 70ЁмxЃМ80 | 9 | b |
Ек4ЖЮ | 80ЁмxЃМ90 | a | 0.36 |
Ек5ЖЮ | 90ЁмxЁм100 | 15 | 0.30 |
ЧыИљОнЫљИјаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉaЃН______ЃЌbЃН______ЃЛ
ЃЈ2ЃЉЧыВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉбљБОжаЃЌВПЗжбЇЩњГЩМЈЕФжаЮЛЪ§ТфдкЕк_______ЖЮЃЛ
ЃЈ4ЃЉвбжЊИУФъМЖга400УћбЇЩњВЮМгетДЮБШШќЃЌШєГЩМЈдк90ЗжвдЩЯЃЈКЌ90ЗжЃЉЕФЮЊгХЃЌЙРМЦИУФъМЖГЩМЈЮЊгХЕФгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌфПфПвЛМвМнГЕДгAЕиГіЗЂЃЌбизХББЦЋЖЋ60ЁуЕФЗНЯђааЪЛЃЌЕНДяBЕиКѓбизХФЯЦЋЖЋ50ЁуЕФЗНЯђааЪЛРДЕНCЕиЃЌCЕиЧЁКУЮЛгкAЕие§ЖЋЗНЯђЩЯЃЌдђЃЈЁЁЁЁЃЉ
ЂйBЕидкCЕиЕФББЦЋЮї50ЁуЗНЯђЩЯЃЛ
ЂкAЕидкBЕиЕФББЦЋЮї30ЁуЗНЯђЩЯЃЛ
ЂлcosЁЯBAC=![]() ЃЛ
ЃЛ
ЂмЁЯACB=50ЁуЃЎЦфжаДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
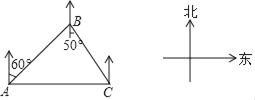
A. ЂйЂк B. ЂкЂм C. ЂйЂл D. ЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХББОЉЩъАьЖЌАТЛсЕФГЩЙІЃЌгњРДгњЖрЕФЭЌбЇПЊЪМЙизЂЮвЙњЕФБљбЉЬхг§ЯюФП. аЁНЁДгаТЮХжаСЫНтЕНЃКдк2018ФъЦНВ§ЖЌАТЛсЕФЖЬЕРЫйЛЌФазг500УзОіШќжаЃЌжаЙњбЁЪжЮфДѓОИвд39Уы584ЕФГЩМЈДђЦЦЪРНчМЭТМЃЌЪеЛёжаЙњФазгЖЬЕРЫйЛЌЖгдкЖЌАТЛсЩЯЕФЪзУЖН№ХЦ. ЭЌФъ11дТ12ШеЃЌЮфДѓОИгжвд39Уы505ЕФГЩМЈдйЦЦЪРНчМЭТМ. гкЪЧаЁНЁЖдЭЌбЇУЧЫЕЃКЁА2022ФъББОЉЖЌАТЛсЩЯЮфДѓОИдйЛёН№ХЦЕФПЩФмадДѓаЁЪЧ![]() .ЁБФуШЯЮЊаЁНЁЕФЫЕЗЈ_________ЃЈЬюЁАКЯРэЁБЛђЁАВЛКЯРэЁБЃЉЃЌРэгЩЪЧ__________________________.
.ЁБФуШЯЮЊаЁНЁЕФЫЕЗЈ_________ЃЈЬюЁАКЯРэЁБЛђЁАВЛКЯРэЁБЃЉЃЌРэгЩЪЧ__________________________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЗНГЬЃК
ЃЈ1ЃЉ3x2ЃЋ8xЃ3=0ЃЛЃЈ2ЃЉx2+3xЃ1=0ЃЛЃЈ3ЃЉx2Ѓ2xЃ3=0ЃЛЃЈ4ЃЉЃЈx+4ЃЉ2=5ЃЈx+4ЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com