
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】我市开展“美丽泰安,创卫同行”活动,某校倡议学生利用双休日在某公园参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息可知扇形图中的“1.5小时”部分圆心角的度数是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距80km,一辆汽车上午9:00从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了20km/h,并继续匀速行驶至乙地,汽车行驶的路程y(km)与时间x(h)之间的函数关系如图所示,该车到达乙地的时间是当天上午( )
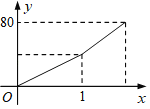
A. 10:35 B. 10:40 C. 10:45 D. 10:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠EAD=∠C.

(1)试判断AE与CD的位置关系,并说明理由;
(2)若∠FEC=∠BAE,∠EFC=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把6张长为a、宽为b(a>b)的小长方形纸片不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设这两个长方形的面积的差为S.当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b满足( )

A. a=1.5bB. a=2.5bC. a=3bD. a=2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(提高题) 如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.
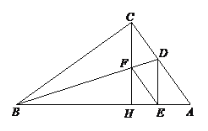
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com