
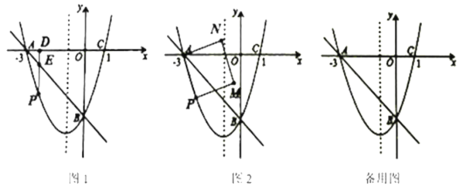
【题目】如图1,抛物线y = ax2+bx-3经过A、B、C三点,己知点A(-3,0)、C (1, 0).
(1)求此抛物线的解析式.
(2)点P是直线AB下方的抛物线上一动点(不与A、B重合),
①过点F作x轴的垂线,垂足为D,交直线AB于点E,动点P在什么位置时,PE最大,求 出此时P点的坐标.
②如图2,连接AP.以AP为边作图示一侧的正方形APMN,当它恰好有一个顶点落在抛物 线对称轴上时,求出对应的P点的坐标.
【答案】(1)y = x2+2x﹣3;(2)①(﹣![]() ,
,![]() ),②(﹣
),②(﹣![]() -1,2)或(
-1,2)或(![]() ,
,![]() )
)
【解析】
(1)直接用待定系数法求解即可;
(2)①由抛物线解析式y = x2+2x﹣3,令x=0,y=﹣3,求出点B(0,-3),设直线AB的解析式为y=kx+b,把A(﹣3,0)和B(0,﹣3)代入y =kx+b求出k=-1,b=-3,直线AB的解析式为y=﹣x﹣3,设E(x,﹣x﹣3),则PE=﹣(x+![]() )2+
)2+![]() ,从而得当PE最大时,P点坐标为(﹣
,从而得当PE最大时,P点坐标为(﹣![]() ,
,![]() );
);
②抛物线对称轴为直线x=﹣1,A(﹣3,0),正方形APMN的顶点落在抛物线对称轴上的情况有两种情况,i) 当点N在抛物线对称轴直线x=﹣1上;ii)当点M在抛物线对称轴直线x=﹣1;根据这两种情况,作出图形,找到线段之间的等量关系,解之即可..
(1)把A(﹣3,0)和C(1,0)代入y = ax2+bx﹣3得,
![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y = x2+2x﹣3;
(2)设P(x,x2+2x﹣3),直线AB的解析式为y=kx+b,
①由抛物线解析式y = x2+2x﹣3,令x=0,y=﹣3,
∴B(0,﹣3),
把A(﹣3,0)和B(0,﹣3)代入y =kx+b得,
![]() 解得
解得![]() ,
,
∴直线AB的解析式为y=﹣x﹣3,
∵PE⊥x轴,
∴E(x,﹣x﹣3),
∵P在直线AB下方,
∴PE=﹣x﹣3﹣( x2+2x﹣3)=﹣x2﹣3x=﹣(x+![]() )2+
)2+![]() ,
,
当x=﹣![]() 时,y= x2+2x﹣3=
时,y= x2+2x﹣3=![]() ,
,
∴当PE最大时,P点坐标为(﹣![]() ,
,![]() ).
).
②抛物线对称轴为直线x=﹣1,A(﹣3,0),正方形APMN的顶点落在抛物线对称轴上的情况有两种:
i)当点N在抛物线对称轴直线x=﹣1上时,作PR⊥x轴于点R,设对称轴与x轴的交点为L,如图①,
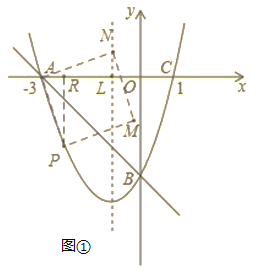
∵四边形APMN为正方形,
∴AN=AP,∠PAR+∠RAN=90°,
∵∠PAR+∠APR=90°,
∴∠APR=∠RAN,
在△APR和△NAL中
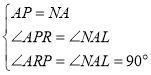
∴△APR≌△NAL(AAS),
∴PR=AL,
∵AL=﹣1-(﹣3)=2,
∴PR=2,此时 x2+2x﹣3=2,解得x1=![]() -1,x2=﹣
-1,x2=﹣![]() -1,
-1,
∵P在直线AB下方,
∴x=﹣![]() -1,
-1,
∴P(﹣![]() -1,2);
-1,2);
ii)当点M在抛物线对称轴直线x=﹣1上时,如图②,过点P作PH⊥对称轴于点H、作AG⊥HP于点G,
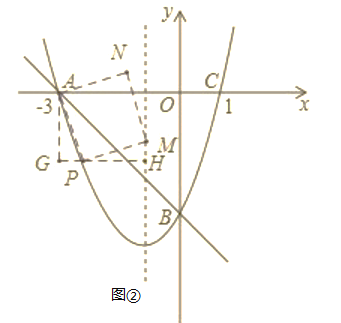
∵四边形APMN为正方形,
∴PA=PM,∠APM=90°,
∴∠APG+∠MPH=90°,
∵∠APG+∠GAP=90°,
∴∠GAP=∠HPM,
在△APG和△PMH中
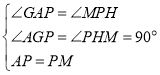
∴△APG≌△PMH(AAS),
∴AG=PH,PG=MH,
∴GH=PG+PH
∵P(x,x2+2x-3)
∴x+3+(-x2-2x+3)=2,解得x1=![]() ,x2=
,x2=![]() ,
,
∵P在直线AB下方,
∴x=![]() ,
,
∴P(![]() ,
,![]() )
)
终上所述,点P对应的坐标为(﹣![]() -1,2)或(
-1,2)或(![]() ,
,![]() ).
).


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,C,D是⊙O上AB同侧两点,∠BAC=26°.
(Ⅰ)如图1,若OD⊥AB,求∠ABC和∠ODC的大小;
(Ⅱ)如图2,过点C作⊙O的切线,交AB的延长线于点E,若OD∥EC,求∠ACD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
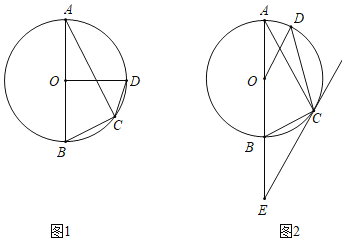
【题目】周末,小马和小聪想用所学的数学知识测量图书馆前小河的宽,测量时,他们选择河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.35m,BD=7m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:如图①,若点D在△ABC的边AB上,且满足∠ACD=∠B(或∠BCD=∠A),则称满足这样条件的点为△ABC边AB上的“理想点”.
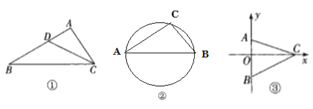
(1)如图①,若点D是△ABC的边AB的中点,AC=![]() ,AB=4.试判断点D是不是△ABC边AB上的“理想点”,并说明理由.
,AB=4.试判断点D是不是△ABC边AB上的“理想点”,并说明理由.
(2)如图②,在⊙O中,AB为直径,且AB=5,AC=4.若点D是△ABC边AB上的“理想点”,求CD的长.
(3)如图③,已知平面直角坐标系中,点A(0,2),B(0,-3),C为x轴正半轴上一点,且满足∠ACB=45°,在y轴上是否存在一点D,使点A是B,C,D三点围成的三角形的“理想点”,若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
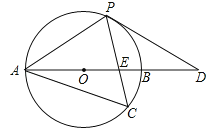
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CECP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月21日,重庆市第八届中小学艺术工作坊在渝北区空港新城小学体育馆开幕,来自全重庆市各个区县共二十多个工作坊集中展示了自己的艺术特色.组委会准备为现场展示的参赛选手购买三种纪念品,其中甲纪念品5元/件,乙纪念品7元/件,丙纪念品10元/件.要求购买乙纪念品数量是丙纪念品数量的2倍,总费用为346元.若使购买的纪念品总数最多,则应购买纪念品共_____件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D,E分别是AB,BC边上的点,且DE∥AC,若![]() ,
,![]() ,则△ACD的面积为( )
,则△ACD的面积为( )
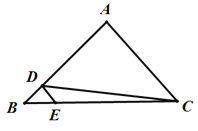
A. 64 B. 72 C. 80 D. 96
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com