
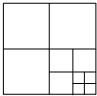
 如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.| 操作次数N | 1 | 2 | 3 | 4 | 5 | … | n |
| 正方形个数 | 4 | 7 | 10 | an |
分析 (1)(2)分别数出图1、图2、图3中正方形的个数,可以发现第几个图形中正方形的个数等于3与几的乘积加1;按照这个规律即可求得正方形的个数an和操作次数n之间的关系;
(3)然后将2015代入,如果得数为整数,正方形的个数能为2015个;如果得数不是整数,正方形的个数不能为2015个.
解答 解:(1)图1中正方形的个数为4=3×1+1;
图2中正方形的个数为7=3×2+1;
图3中正方形的个数为10=3×3+1;
…
可以发现:图几中正方形的个数等于3与几的乘积加1.
可得,图4、图5中正方形的个数分别为13、16.
| 操作次数N | 1 | 2 | 3 | 4 | 5 | … | n |
| 正方形个数 | 4 | 7 | 10 | 13 | 16 | an |
点评 此题主要考图形变化规律,解答此类题目的关键是根据题目中给出的图形,数值等条件,认真分析,找到规律,解决问题.


科目:初中数学 来源: 题型:解答题
| 原料型号 | A | B | C |
| 每辆车的装载重量(吨) | 2 | 1 | 1.5 |
| 每辆车的运输费用(元 | 50 | 70 | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:在Rt△OAB中,∠OAB=90°,若以D为坐标原点,OA所在直线为x轴,建立如图的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处,点C(3,4).
已知:在Rt△OAB中,∠OAB=90°,若以D为坐标原点,OA所在直线为x轴,建立如图的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处,点C(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,对角线AC,BD交于点O,EF是过点O的一条直线,交AB于点E,交DC于点F.请写出图中的一对全等三角形是△DOF≌△BOE.
如图,在?ABCD中,对角线AC,BD交于点O,EF是过点O的一条直线,交AB于点E,交DC于点F.请写出图中的一对全等三角形是△DOF≌△BOE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
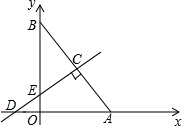 如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴,y轴的正半轴上,且A(6,0),cos∠BAO=$\frac{3}{5}$,线段AB的垂直平分线CD交AB于点C,交y轴于点E,交x轴于点D.
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA,OB分别在x轴,y轴的正半轴上,且A(6,0),cos∠BAO=$\frac{3}{5}$,线段AB的垂直平分线CD交AB于点C,交y轴于点E,交x轴于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com