Question

10．△ACB和△ECD是以点C为公共顶点的等腰直角三角形，∠ACB=∠ECD=90°，连接AD，BE，点F为BE的中点，连接CF．
（1）如图①，当∠ACB与∠ECD重合时，线段AD与CF的位置关系是AD⊥CF，数量关系是AD=2CF；
（2）如图②，当∠ACB与∠ECD不重合时，判断（1）中结论还成立吗？如果成立，请加以证明；如果不成立，请说明理由；
（3）如图③，当△ECD的斜边DE与点A在一条直线上时，若AC=3，CE=$\sqrt{2}$，求CF的长（直接写出结果）

Answer 1

分析 （1）方法1、先判断出△BCE≌△DCG（SAS），得出∠CBE=∠CGH，BE=DG，进而判断出BF=GH，即可判断出△BCF≌△GCH（SAS），得出CF=CH，再判断出CH是△ADG的中位线，即可得出结论；
方法2、CF是BE的一半，直角三角形斜边中线的特点，再只要证BE=AD即可，证△ADE全等三角形BEC，即可得出结论，
（2）先判断出∠BCE=∠GCD，即可判断出△BCF≌△GCH（SAS），其余同（1）的方法即可得出结论；
（3）同（2）的方法得出AD⊥AF，AD=2CF，根据等腰直角三角形的性质得出CM=DM=1，再在Rt△ACM中，根据勾股定理得出AM=2$\sqrt{2}$，即可得出AD=2$\sqrt{2}$+1即可．

解答 解：（1）方法1、如图①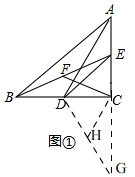，延长AG至G使CG=AC，连接DG，
∴∠ACB=∠GCD，
∵BC=AC，
∴BC=CG，
在△BCE和△DCG中，$\left\{\begin{array}{l}{CE=CD}\\{∠BCE=∠GCD}\\{BC=CG}\end{array}\right.$，
∴△BCE≌△DCG（SAS），
∴∠CBE=∠CGH，BE=DG，
∵点F为BE的中点，
∴BF=$\frac{1}{2}$BE，
取DG的中点H，连接CH，
∴GH=DH=$\frac{1}{2}$DG，
∴BF=GH，
在△BCF和△GCH中，$\left\{\begin{array}{l}{BF=GF}\\{∠CBF=∠CGH}\\{BC=CG}\end{array}\right.$，
∴△BCF≌△GCH（SAS），
∴CF=CH，∠BCF=∠GCH，
∴∠FCH=∠BCF+∠DCH=∠GCH+∠DCH=∠DCG=90°，
∴CF⊥CH，
∵AC=CG，DH=GH，
∴CH是△ADG的中位线，
∴CH=$\frac{1}{2}$AD，CH∥AD，
∵CF=CH，
∴CF=$\frac{1}{2}$AD，
∴AD=2CF，
∵CH∥AD，CF⊥CH，
∴CF⊥AD；
故答案为：AD⊥CF，AD=2CF，
方法2\
∵△ABC，△CDE是等腰直角三角形，
∴BC=AC，CD=CE，∠BCE=∠ACD，
∴△BCE≌△ACD，
∴∠CBE=∠CAD，BE=AD，
∵CF是Rt△BCE是直角三角形的斜边的中线，
∴BE=2CF=2BF，
∴AD=2CF，
∵BF=CF，
∴∠CBE=∠BCF，
∵∠CBE=∠CAD，
∴∠BCF=∠CAD，
∵∠BCF+∠ACF=90°，
∴∠CAD+∠ACF=90°，
∴AD⊥CF；

（2）（1）中结论仍然成立，即：AD⊥CF，AD=2CF，
理由：如图②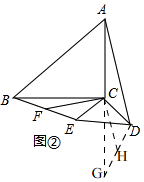，延长AG至G使CG=AC，连接DG，
∴∠BCG=90°，∵∠DCE=90°，
∴∠BCE=∠GCD，
∵BC=AC，
∴BC=CG，
在△BCE和△DCG中，$\left\{\begin{array}{l}{CE=CD}\\{∠BCE=∠GCD}\\{BC=CG}\end{array}\right.$，
∴△BCE≌△DCG（SAS），
∴∠CBE=∠CGH，BE=DG，
∵点F为BE的中点，
∴BF=$\frac{1}{2}$BE，
取DG的中点H，连接CH，
∴GH=DH=$\frac{1}{2}$DG，
∴BF=GH，
在△BCF和△GCH中，$\left\{\begin{array}{l}{BF=GF}\\{∠CBF=∠CGH}\\{BC=CG}\end{array}\right.$，
∴△BCF≌△GCH（SAS），
∴CF=CH，∠BCF=∠GCH，
∴∠FCH=∠BCF+∠DCH=∠GCH+∠DCH=∠DCG=90°，
∴CF⊥CH，
∵AC=CG，DH=GH，
∴CH是△ADG的中位线，
∴CH=$\frac{1}{2}$AD，CH∥AD，
∵CF=CH，
∴CF=$\frac{1}{2}$AD，
∴AD=2CF，
∵CH∥AD，CF⊥CH，
∴CF⊥AD；
即：AD⊥CF，AD=2CF，

（3）如图③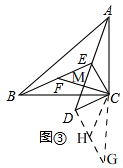，同（2）得出AD⊥AF，AD=2CF，
∵△CDE是等腰直角三角形，
∴CD=CE=$\sqrt{2}$，
∴DE=$\sqrt{2}$CE=2，
在等腰Rt△CDE中，CF⊥AD于M，
∴DM=EM=CM=$\frac{1}{2}$DE=1，
∵△ECD的斜边DE与点A在一条直线上，
在Rt△ACM中，AC=3，CM=1，
根据勾股定理得，AM=$\sqrt{A{C}^{2}-C{M}^{2}}$=2$\sqrt{2}$，
∴AD=AM+DM=2$\sqrt{2}$+1，
∴CF=$\frac{1}{2}$AD=$\frac{2\sqrt{2}+1}{2}$=$\sqrt{2}$+$\frac{1}{2}$．

点评 此题是三角形的综合题，主要考查了全等三角形的判定和性质，三角形的中位线的判定和性质，垂直的判定；作出辅助线构造出△BCE≌△DCG（SAS）和△BCF≌△GCH（SAS）是解本题的关键，也是解本题的难点．