
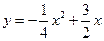 的图象如图.
的图象如图.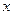 轴交点D的坐标;
轴交点D的坐标;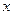 轴,
轴,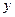 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
 解: (1)由
解: (1)由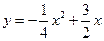 得
得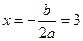 …………1分
…………1分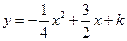 …………3分
…………3分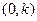 OC=
OC=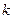
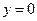 即
即 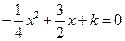
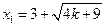
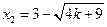 …………4分
…………4分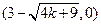 ,B
,B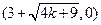
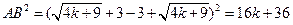 ………5分
………5分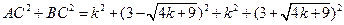
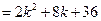 ……………………6分
……………………6分

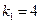
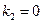 (舍去) ……………7分
(舍去) ……………7分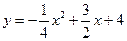 ……………8分
……………8分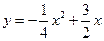 ∴顶点坐标
∴顶点坐标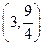
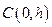 ,顶点坐标
,顶点坐标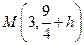 …………3分
…………3分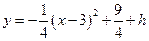 ……………………4分
……………………4分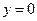 时,
时,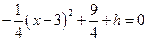 , 得
, 得 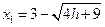
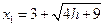
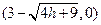 B
B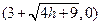 ……………………5分
……………………5分 OA·OB……………………6分
OA·OB……………………6分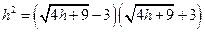 得
得 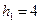 ,
,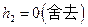 …………7分
…………7分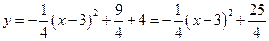 …………8分
…………8分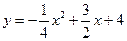 可得
可得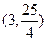 …………9分
…………9分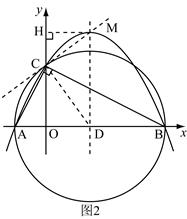 过C、M作直线,连结CD,过M作MH垂直y轴于H,
过C、M作直线,连结CD,过M作MH垂直y轴于H,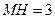
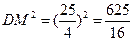
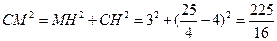
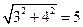 =AD
=AD 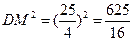
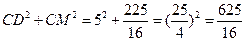 ……11分
……11分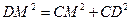
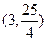 …………9分
…………9分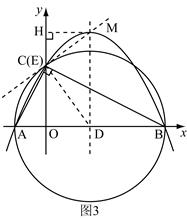 作直线CM,过D作DE⊥CM于E, 过M作MH垂直y轴于H,则
作直线CM,过D作DE⊥CM于E, 过M作MH垂直y轴于H,则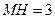 ,
, 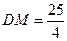 , 由勾股定理得
, 由勾股定理得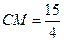
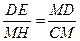 得
得 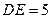 …………11分
…………11分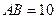 ∴⊙D的半径为5
∴⊙D的半径为5 

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
(本题满分12分)
已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=r2
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2011年滨海新区大港初中毕业生学业考试第一次模拟试卷数学 题型:解答题
(本题满分12分)已进入汛期,7年级1班的同学到水库调查了解汛情。水库一
共有10个泄洪闸,现在水库水位已超过安全线,上游的河水仍以一个不变的速度流入水库。
同学们经过一天的观察和测量,做了如下记录:上午打开一个泄洪闸,在2小时内水位继续
上涨了0.06米;下午再打开2个泄洪闸后,4小时内水位下降了0.1米。目前水位仍超过安
全线1.2米。
(1)如果打开5个泄洪闸,还需几个小时水位降到安全线?
(2)如果防汛指挥部要求在6小时内使水位降到安全线,应该再打开几个泄洪闸?
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省宿迁市)九年级第二次联考数学试卷(解析版) 题型:解答题
(本题满分12分)
已知:如图, 为平行四边形ABCD的对角线,
为平行四边形ABCD的对角线, 为
为 的中点,
的中点, 于点
于点 ,与
,与 ,
, 分别交于点
分别交于点 .
.

求证:⑴ .
.
⑵
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省苏州市九年级10月月考数学卷 题型:解答题
(本题满分12分)已知,AB为⊙O 的直径,点E 为弧AB 任意一点,如图,AC平分∠BAE,交⊙O于C ,过点C作CD⊥AE于D,与AB的延长线交于P.

⑴ 求证:PC是⊙O的切线.⑵ 若∠BAE=60°,求线段PB与AB的数量关系.
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省扬州市九年级第一学期期末考试数学卷 题型:解答题
(本题满分12分)
已知直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.

1.(1)填空:菱形ABCD的边长是 ▲ 、面积是 ▲ 、 高BE的长是 ▲ ;
2.(2)探究下列问题:
若点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时
② △APQ的面积S关于t的函数关系式,以及S的最大值;
3.(3)在运动过程中是否存在某一时刻使得△APQ为等腰三角形,若存在求出t的值;若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com