
【题目】如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( ) 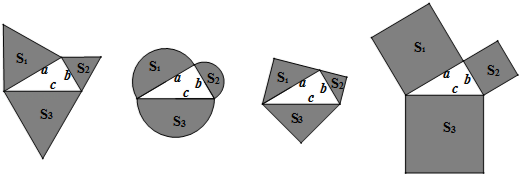
A.1
B.2
C.3
D.4
【答案】D
【解析】解:(1)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 , ∵a2+b2=c2 ,
c2 , ∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 . (2)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 ,
c2 ,
∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 . (3)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 ,
c2 ,
∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 . (4)S1=a2 , S2=b2 , S3=c2 ,
∵a2+b2=c2 ,
∴S1+S2=S3 .
综上,可得
面积关系满足S1+S2=S3图形有4个.
故选:D.
根据直角三角形a、b、c为边,应用勾股定理,可得a2+b2=c2 . (1)第一个图形中,首先根据等边三角形的面积的求法,表示出3个三角形的面积;然后根据a2+b2=c2 , 可得S1+S2=S3 . (2)第二个图形中,首先根据圆的面积的求法,表示出3个半圆的面积;然后根据a2+b2=c2 , 可得S1+S2=S3 . (3)第三个图形中,首先根据等腰直角三角形的面积的求法,表示出3个等腰直角三角形的面积;然后根据a2+b2=c2 , 可得S1+S2=S3 . (4)第四个图形中,首先根据正方形的面积的求法,表示出3个正方形的面积;然后根据a2+b2=c2 , 可得S1+S2=S3 .


科目:初中数学 来源: 题型:
【题目】如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个性状、大小相同的大长方形内放入四个如图③的小长方形后得图①、图②,已知大长方形的长为a,则图①阴影部分的周长与图②阴影部分的周长的差是 . (用含a的代数式表示) 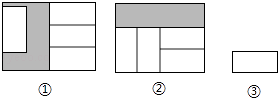
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A,B,C,D,E分别位于如图所示的小正方形格点上.
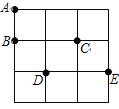
(1)在点A,B,C,D,E中任取四个点为顶点直接在图上画一个中心对称的四边形;
(2)从A,B,C三个点中先任取一个点,在余下的两个点中再取一个点,将所取的这两点与点D,E为顶点构成四边形,求所得四边形中面积为2的概率(用树状图或列表法求解).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com