
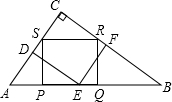
| x |
| 4 |
| 3-x |
| 3 |
| 12 |
| 7 |
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
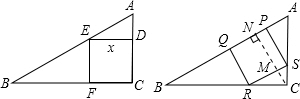
| SR |
| AB |
| CM |
| CN |
| ||
|
| y |
| 5 |
| 60 |
| 37 |
| 12 |
| 7 |
| 60 |
| 37 |
| 444-420 |
| 7×37 |


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
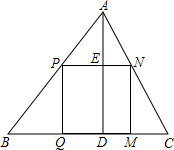 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形一边在BC上,其余两个顶点分别在AB,AC上,那么这个正方形零件的边长应是
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形一边在BC上,其余两个顶点分别在AB,AC上,那么这个正方形零件的边长应是查看答案和解析>>
科目:初中数学 来源: 题型:
 19、如图:△ABC是一块直角三角形余料,∠C=90度,工人师傅把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上,请你协助工人师傅用尺规画出裁割线.(不写画法,保留作图痕迹)
19、如图:△ABC是一块直角三角形余料,∠C=90度,工人师傅把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上,请你协助工人师傅用尺规画出裁割线.(不写画法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是一块锐角三角形材料,边BC=6cm,高AD=4cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,要使矩形EGFH的面积最大,EG的长应为
如图,△ABC是一块锐角三角形材料,边BC=6cm,高AD=4cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,要使矩形EGFH的面积最大,EG的长应为查看答案和解析>>
科目:初中数学 来源: 题型:
 19、如图,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上.
19、如图,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,则四边形DEFG最大面积为( )cm2.
如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,则四边形DEFG最大面积为( )cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com