
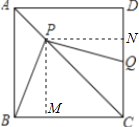
【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4![]() ,CQ=10,则正方形ABCD的面积为 .
,CQ=10,则正方形ABCD的面积为 .

【答案】324
【解析】
试题分析:作PM⊥BC于点M,PN⊥CD于点N,利用正方形的性质和角平分线上的点到角的两边相等以及已知条件即可证明△BPM≌△QPN,得出BM=QN,设BM=x,则NF=x,PM=CM=CN=10+x,根据平行线分线段成比例定理即可得到关于x的比例式,求出x的值,即可求出正方形的边长,进而求出其面积.
解:作PM⊥BC于点M,PN⊥CD于点N,如图所示:
∵四边形ABCD是正方形,
∴AC平分∠BCD,
∴PM=PN,∠NEM=90°,
∴四边形PMCN为正方形,∵PQ⊥BP,∴∠BPQ=90°,
∴∠BPM=∠NPQ,
在△BPM和△QPN中,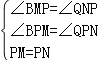 ,
,
∴△BPM≌△QPN(AAS),
∴BM=QN;
设BM=x,则NF=x,
∴PM=CM=CN=10+x,
∴CP=![]() (10+x),
(10+x),
∵PM∥AB,
∴![]() ,即
,即![]() ,
,
解得:x=4或x=﹣10(舍),
∴BM=4,CM=14,
∴BC=BM+CM=18,
∴正方形ABCD的面积为:18×18=324.
故答案为:324.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.

(1)当AC的长度为多少时,△AMC和△BOD相似;
(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;
(3)连结BC.当S△AMC=S△BOC时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD.

(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若![]() :
:![]() =1:2,求AE:EB:BD的值(请你直接写出结果);
=1:2,求AE:EB:BD的值(请你直接写出结果);
(3)若点C是弧AB的中点,已知AB=4,求CE![]() CP的值.
CP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n是关于x的一元二次方程x2﹣3x+a=0的两个解,若(m﹣1)(n﹣1)=﹣6,则a的值为( )
A.﹣10 B.4 C.﹣4 D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店今年1﹣6月份经营A、B两种电子产品,已知A产品每个月的销售数量y(件)与月份x(1≤x≤6且x为整数)之间的关系如表今年1﹣6月份经营A、B两种电子产品,已知A产品 每个月的销售数量y(件)与月份x(1≤x≤6且x为整数)之间的关系如表
x 1 2 3 4 5 6
y 600 300 200 150 120 100
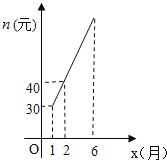
A产品每个月的售价z(元)与月份x之间的函数关系式为:z=10x,已知B产品每个月的销售数量m(件)与月份x之间的关系为:m=﹣2x+62,B产品每个月的售价n(元)与月份x存在如图所示的变化趋势.
(1)请观察题中表格,用所学过的一次函数或反比例函数的有关知识,直接写出y与x的函数关系式
(2)请观察如图所示的变化趋势,求出n与x的函数关系式
(3)求出此商店1﹣6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式
(4)今年7月份,商店调整了A、B两种电子产品产品的价格,A产品价格在6月份基础上增加a%,B产品价格在6月份基础上减少a%,结果7月份A产品的销售数量比6月份减少2a%,B产品的销售数量比6月份增加2a%,若调整价格后7月份的销售总额比6月份的销售总额少2000元,请根据以下参考数据估算a的值.(参考数据:6.32=39.69,6.42=40.91,6.52=42.25,6.62=43.56)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
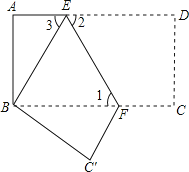
(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com