
分析 (1)将${(\frac{1}{4})^{-1}}$=4,|${-\sqrt{3}}$|=$\sqrt{3}$,(π-3)0=1,tan30°=$\frac{\sqrt{3}}{3}$代入到原式,再利用实数的运算法则即可得出结论;
(2)解不等式组得出3≤x<5,从而得出结论.
解答 解:(1)原式=4+$\sqrt{3}$-1+3×$\frac{\sqrt{3}}{3}$,
=4+$\sqrt{3}$-1+$\sqrt{3}$,
=3+2$\sqrt{3}$.
故答案为:3+2$\sqrt{3}$.
(2)解$\left\{\begin{array}{l}{x-2≥1}\\{2(x-1)<x+3}\end{array}$,得$\left\{\begin{array}{l}{x≥3}\\{x<5}\end{array}\right.$,
即3≤x<5.
故该不等式组的最大整数解是4.
点评 本题考查了实数的运算、零指数幂、负整数指数幂、特殊角的三角函数值以及解一元一次不等式组,解题的关键是:(1)将${(\frac{1}{4})^{-1}}$=4,|${-\sqrt{3}}$|=$\sqrt{3}$,(π-3)0=1,tan30°=$\frac{\sqrt{3}}{3}$代入到原式;(2)能熟练解一元一次不等式组.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
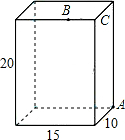 如图,一个无盖的长方体盒子的长为15cm,宽为10cm,高为20cm,点B离点C的距离为
如图,一个无盖的长方体盒子的长为15cm,宽为10cm,高为20cm,点B离点C的距离为查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平面直角坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第2个正方形A1B1C1C;延长C1B1交x轴于点A2,作第3个正方形A2B2C2C1…按这样的规律进行下去,第2个正方形的面积为45;第2015个正方形的面积为20×$(\frac{9}{4})$2014.
在平面直角坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第2个正方形A1B1C1C;延长C1B1交x轴于点A2,作第3个正方形A2B2C2C1…按这样的规律进行下去,第2个正方形的面积为45;第2015个正方形的面积为20×$(\frac{9}{4})$2014.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
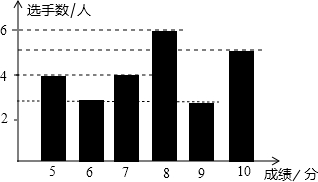 某校举行学生“爱校•爱家•爱国”主题演讲比赛,某同学将选手们的得分进行统计,绘制成如图所示的得分条形图下列四个判断:
某校举行学生“爱校•爱家•爱国”主题演讲比赛,某同学将选手们的得分进行统计,绘制成如图所示的得分条形图下列四个判断:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m-2>n-2 | B. | $\frac{m}{2}>\frac{n}{2}$ | C. | -2m>-2n | D. | m+2>n+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com