
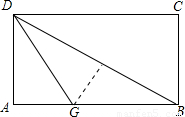
如下图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=2,BC=1,则AG的长是__________。
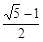
【解析】
试题分析:已知AB=2,BC=1,可知AD=BC=1,在Rt△ABD中根据勾股定理求得BD的长;设AG=x,由折叠的性质可知,GH=x,BH=BD-DH=BD-AD=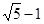 ,BG=2-x,在Rt△BGH中,根据勾股定理列方程求解即可.
,BG=2-x,在Rt△BGH中,根据勾股定理列方程求解即可.
由题意得AB=2,AD=BC=1,
在Rt△ABD中,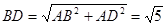 ,
,
过点G作GH⊥BD,垂足为H,
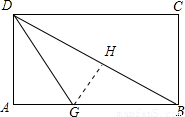
由折叠可知:△AGD≌△HGD,
∴AD=DH=1,设AG的长为x,HG=AG=x,BG=2-x,BH=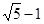 ,
,
在Rt△BGH中,由勾股定理得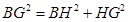
即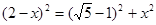
解得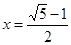
则AG的长是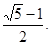
考点:本题考查图形的翻折变换,勾股定理
点评:解答本题的关键是熟练掌握折叠的性质,折叠前后图形的形状和大小不变.


科目:初中数学 来源:初中数学解题思路与方法 题型:044
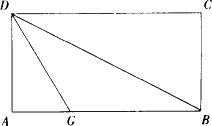
如下图,折叠矩形纸片ABCD,折出折痕(对角线BD),再折叠使AD边与对角线BD重合,得折痕DG,若AB=2,BC=1,求AG的长.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年山西省农业大学附属中学八年级第三次月考数学试卷(带解析) 题型:填空题
如下图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=2,BC=1,则AG的长是__________。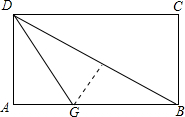
查看答案和解析>>
科目:初中数学 来源:期末题 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com