
【题目】已知:点C为∠AOB内一点.
(1)在OA上求作点D,在OB上求作点E,使△CDE的周长最小,请画出图形;(不写做法,保留作图痕迹)
(2)在(1)的条件下,若∠AOB=30°,OC=10,求△CDE周长的最小值.

【答案】(1)见解析;(2)△CDE周长的最小值为10.
【解析】
(1)分别作C点关于OA、OB的对称点M、N,然后连接MN分别交OA、OB于D、E,利用两点之间线段最短可判断此时△CDE的周长最小;
(2)利用对称的性质得到OM=OC=10,∠MOA=∠COA,ON=OC=10,∠NOB=∠COB,则△DCE的周长为MN,再证明△OMN为等边三角形,从而得到MN=OM=10,所以△CDE周长的最小值为10.
(1)如图,△CDE为所作;
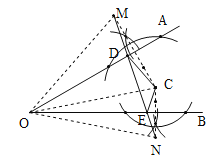
(2)∵点M与点C关于OA对称,
∴OM=OC=10,∠MOA=∠COA,DM=DC.
∵点N与点C关于OB对称,
∴ON=OC=10,∠NOB=∠COB,EC=EN,
∴△DCE的周长为CD+CE+DE=DM+DE+EN=MN,
∴此时△DCE的周长最小.
∵∠MOA+∠NOB=∠COA+∠COB=∠AOB=30°,
∴∠MON=30°+30°=60°,
∴△OMN为等边三角形,
∴MN=OM=10,
∴△CDE周长的最小值为10.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,估计下列事件发生的可能性的大小,并将这些事件的序号按发生的可能性从小到大的顺序排成一列是__________.(填序号)

(1)指针落在标有3的区域内;(2)指针落在标有9的区域内;
(3)指针落在标有数字的区域内;(4)指针落在标有奇数的区域内.
查看答案和解析>>
科目:初中数学 来源: 题型:
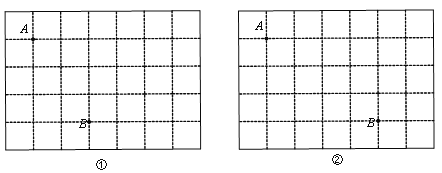
【题目】如图①、图②,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点,图①和图②中的点A、点B都是格点.分别在图①、图②中画出格点C,并满足下面的条件:
(1)在图①中,使∠ABC=90°.此时AC的长度是 .
(2)在图②中,使AB=AC.此时△ABC的边AB上的高是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
![]() 从今年年初至
从今年年初至![]() 月
月![]() 日,猪肉价格不断走高,
日,猪肉价格不断走高,![]() 月
月![]() 日比年初价格上涨了
日比年初价格上涨了![]() .某市民在今年
.某市民在今年![]() 月
月![]() 日购买
日购买![]() 千克猪肉至少要花
千克猪肉至少要花![]() 元钱,那么今年年初猪肉的最低价格为每千克多少元?
元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)![]() 月
月![]() 日,猪肉价格为每千克
日,猪肉价格为每千克![]() 元
元![]() 月
月![]() 日,某市决定投入储备猪肉并规定其销售价在每千克
日,某市决定投入储备猪肉并规定其销售价在每千克![]() 元的基础上下调
元的基础上下调![]() 出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克
出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克![]() 元的情况下,该天的两种猪肉总销量比
元的情况下,该天的两种猪肉总销量比![]() 月
月![]() 日增加了
日增加了![]() ,且储备猪肉的销量占总销量的
,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比
,两种猪肉销售的总金额比![]() 月
月![]() 日提高了
日提高了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
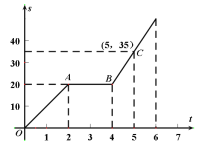
【题目】小明骑自行车从甲地到乙地,图中的折线表示小明行驶的路程![]() 与所用时间
与所用时间![]() 之间的函数关系.试根据函数图像解答下列问题:
之间的函数关系.试根据函数图像解答下列问题:
(1)小明在途中停留了____![]() ,小明在停留之前的速度为____
,小明在停留之前的速度为____![]() ;
;
(2)求线段![]() 的函数表达式;
的函数表达式;
(3)小明出发1小时后,小华也从甲地沿相同路径匀速向乙地骑行,![]()
![]() 时,两人同时到达乙地,求
时,两人同时到达乙地,求![]() 为何值时,两人在途中相遇.
为何值时,两人在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
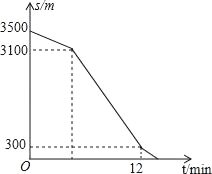
【题目】小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计).一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有4分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离s(单位:米)与他所用的时间t(单位:分钟)之间的函数关系如图所示.已知小刚从家出发7分钟时与家的距离是1200米,从上公交车到他到达学校共用10分钟.下列说法:
①公交车的速度为400米/分钟;
②小刚从家出发5分钟时乘上公交车;
③小刚下公交车后跑向学校的速度是100米/分钟;
④小刚上课迟到了1分钟.
其中正确的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在反比例函数y=![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA于点M,求∠BMC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com