
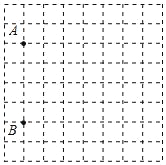
����Ŀ��ʮһ�ڼ䣬С��һ��һ��ȥ���Σ���ͼ��С����Ƶ�ij���ξ����ͼֽ������������ͬ��С��������ɵģ���С�����εı߳�����ʵ�ʳ���100m���ڸ�ͼֽ�Ͽɿ���������־�Ծ���A��B���������ʵ���ƽ��ֱ������ϵ�����A����3��1����B����3����3��������������C��1��3����λ��������
��1������ͼ�л���ƽ��ֱ������ϵ�����������C��λ�ã�
��2��ƽ��ֱ������ϵ������ԭ��Ϊ��O����ACO��ֱ�������������жϲ�˵�����ɣ�
���𰸡���1������������2����ACO��ֱ�������Σ�
��������
(1)����A����������ƽ��3����λ�õ��ĵ���y�ᣬ����ƽ��1����λ�õ��ĵ���x�ᣬ�ɵ�ƽ��ֱ������ϵ������C�����꣬�ɵô𰸣�
(2)���ݹ��ɶ��������ACO�������ߣ�Ȼ�����ù��ɶ������涨���ж���ֱ��������.
��1����ͼ:
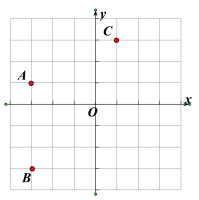
��2����ACO��ֱ�������Σ�
�������£�
��A����3��1����C��1��3����
��OA=![]() =
=![]() ��OC=
��OC=![]() =
=![]() ��AC=
��AC=![]() =2
=2![]() ��
��
��OA2+OC2=AC2��
���AOC��ֱ�������Σ���AOC=90�㣮
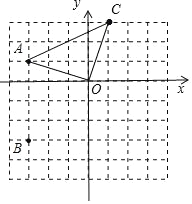
�ʴ�Ϊ����1������������2����ACO��ֱ��������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC����������A��B������ֱ�Ϊ����2��0��������1��0����BC��x�ᣬ����ABC��y��Ϊ�Գ�������ԳƱ任���õ���A��B��C�䣨A��A�䣬B��B�䣬C��C��ֱ��Ƕ�Ӧ���㣩��ֱ��y=x+b������A��C�䣬���C��������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������״�������֮�����˱���������û�����٣��ܽᷴ˼���ڹ�Լ������һ����ͼ�еĺ���ͼ��̻����������ٴ��������Ĺ��£�x��ʾ�ڹ�����������е�ʱ�䣬y1��ʾ�ڹ����е�·�̣�y2��ʾ�������е�·�̣���������˵����

���������ٴ���������·��Ϊ1000����
�����Ӻ��ڹ�ͬʱ����������
���ڹ���;����Ϣ��10���ӣ�
��������;��750�������ڹ꣮
������ȷ��˵������ ������������Ϊ��ȷ˵������Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��x��3����x+1����x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C����DΪ���㣮
��1�����B����D�����꣮
��2������BD��CD�������ߵĶԳ�����x�ύ�ڵ�E��
�����߶�BD��һ��P��ʹ��DCP=��BDE�����P�����꣮
������������һ��M����MN��CD����ֱ��CD�ڵ�N��ʹ��CMN=��BDE�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��װ�н�ˮ�ܺͳ�ˮ�ܵ���������ijʱ�̿�ʼ��4������ֻ��ˮ����ˮ��������8�����ڼȽ�ˮ�ֳ�ˮ�����Źرս�ˮ��ֱ�������ڵ�ˮ���꣮����ÿ���ӵĽ�ˮ���ͳ�ˮ�������������������ڵ�ˮ��y����λ��������ʱ��x����λ�����ӣ�֮��IJ��ֹ�ϵ��ͼ����ʾ����ӹرս�ˮ������Ҫ���ٷ��Ӹ������ڵ�ˮǡ�÷��꣮
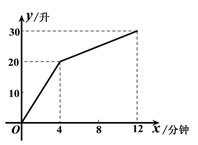
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ע�ⰲȫ����ͬѧ��������ѧ;��һ��Ҫע���ﳵ��ȫ��С���ﵥ����ѧ����������һ��ʱ�䣬����Ҫ��ij���飬�������ۻص��վ������»���꣬��������ȥѧУ�����������������õ�ʱ����·�̵Ĺ�ϵʾ��ͼ������ͼ���ṩ����Ϣ�ش��������⣺

��1��ͼ���Ա�����______,�������______��
��2��С���ҵ�ѧУ��·���� �ף�
��3��С�������ͣ���� ���ӣ�
��4��������ѧ;�У�С��һ����ʻ�� �ף�һ������ ���ӣ�
��5��������Ϊ�ﵥ�����ٶȳ���300��/���Ӿͳ�Խ�˰�ȫ�ȣ��ʣ���������ѧ��;���ĸ�ʱ���С���ﳵ�ٶ���죬�ٶ��ڰ�ȫ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�BE��DF�ֱ��ǡ�ABC����ADC��ƽ���ߣ�����Խ���AC�ֱ��ཻ�ڵ�E��F�� 
��1����֤��AE=CF��
��2������ED��FB���ж��ı���BEDF�Ƿ���ƽ���ı��Σ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��7����ͼ1�ij�Ϊa����Ϊb��a��b����С������ֽƬ����ͼ2�ķ�ʽ���ص��ط��ھ���ABCD�ڣ�δ�����ǵIJ��֣��������Σ�����Ӱ��ʾ�������Ͻ������½ǵ���Ӱ���ֵ�����IJ�ΪS����BC�ij��ȱ仯ʱ������ͬ���ķ��÷�ʽ��Sʼ�ձ��ֲ��䣬��a��b���㣨 �� 
A.a= ![]() b
b
B.a=3b
C.a= ![]() b
b
D.a=4b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ���1��2��22��23��24������22019��ֵ��
�⣺��S��1��2��22��23��24������22018��22019���ٽ���ʽ����ͬʱ��2����
2S��2��22��23��24��25������22019��22020����
����ʽ��ȥ��ʽ����2S��S��22020��1��
��S��22020��1��
��1��2��22��23��24������22019��22020��1.
������մ˷����㣺
(1)1��2��22��23��24������210��
(2)1��3��32��33��34������3n(����n������)��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com