练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】把抛物线y=（x﹣1）2+2向左平移1个单位，再向下平移2个单位，所得抛物线是（ ）
    A.y=x2
    B.y=（x﹣2）2
    C.y=（x﹣2）2+4
    D.y=x2+4

    【答案】A
    【解析】解：∵抛物线y=（x﹣1）2+2的顶点坐标为（1，2），
    ∴向左平移1个单位，再向下平移2个单位后，顶点坐标为（0，0），
    ∴平移后抛物线解析式为y=x2 ．
    故选：A．
    【考点精析】关于本题考查的二次函数图象的平移，需要了解平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，∠1=∠2，AE⊥OB于E，BD⊥OA于D，交点为C，则图中全等三角形共有（ ）

    A.2对
    B.3对
    C.4对
    D.5对

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠A为锐角，且tan35°cotA=1，则∠A=________度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】材料：一般地，n个相同因数a相乘：记为an ． 如23=8，此时，3叫做以2为底的8的对数，记为log28（即log28=3）．那么（log216）2+ log381= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形．如图，就是一组正多边形，观察每个正多边形中∠α的变化情况：

    （1）将下面的表格补充完整：
    （2）根据规律，是否存在一个正多边形，其中的∠α=21°？若存在，请求出n的值，若不存在，请说明理由．

    正多边形边数

    3

    4

    5

    6

    …

    n

    ∠α的度数

    60°

    …

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算
    （1）27﹣19+（﹣7）﹣32；
    （2）（﹣7）÷（﹣ ）×（﹣ ）；
    （3）（ ﹣ + ）×（﹣36）
    （4）﹣14﹣ ×[2﹣（﹣3）2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个整式减去a2﹣b2后所得的结果是﹣a2﹣b2 ， 则这个整式是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个数比x的2倍小3,则这个数可表示为__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请阅读下列材料：

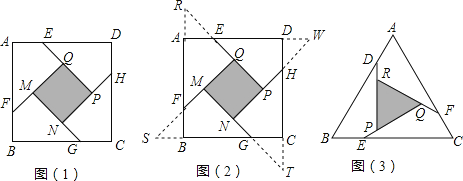
    小明遇到这样一个问题：如图1，在边长为a(a＞2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠GHN=∠DEP=45°时，求正方形MNPQ的面积．

    小明发现，分别延长QE，MF，NG，PH交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形(如图2) ．

    请回答：

    (1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙不重叠)，则这个新正方形的边为 ；

    (2)求正方形MNPQ的面积．

    (3)参考小明思考问题的方法，解决问题：

    如图3，在等边△ABC各边上分别截取AD=BE=CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ．若S△RPQ=，求AD的长．

    查看答案和解析>>

    同步练习册答案