
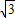 ,求CB的长;
,求CB的长;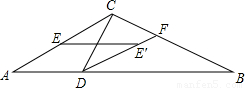
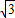 ,CB=BD•cos30°=
,CB=BD•cos30°= ;
; AC根据题中条件证明△BDF∽△BAC,则有
AC根据题中条件证明△BDF∽△BAC,则有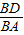 =
=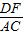 ,BD>AD,
,BD>AD,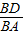 =
=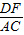 >
> ,DF>
,DF> AC.从而说明所以说E′在线段DF上.
AC.从而说明所以说E′在线段DF上.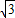 ,
, ;
;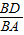 =
=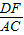 ,
,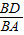 =
=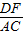 ,>
,> ,
, AC,
AC, AC=AE=DE′,
AC=AE=DE′,

科目:初中数学 来源:2007年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
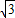 <x2,且抛物线的顶点在直线x=
<x2,且抛物线的顶点在直线x= 的右侧,求a的取值范围.
的右侧,求a的取值范围.查看答案和解析>>
科目:初中数学 来源:2007年福建省厦门市中考数学试卷(解析版) 题型:解答题
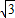 <x2,且抛物线的顶点在直线x=
<x2,且抛物线的顶点在直线x= 的右侧,求a的取值范围.
的右侧,求a的取值范围.查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《圆》(11)(解析版) 题型:解答题
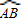 上.
上.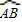 的中点.
的中点.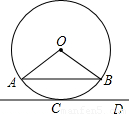
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《四边形》(11)(解析版) 题型:解答题
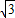 ,求CB的长;
,求CB的长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com