

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源:不详 题型:填空题
 ,测得BC=7m,则桥长AB= m(结果精确到1m
,测得BC=7m,则桥长AB= m(结果精确到1m  =1.414
=1.414  =1.732)
=1.732)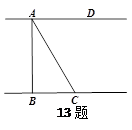
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
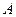 、
、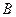 两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段
两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段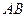 )。经测量,森林保护区中心
)。经测量,森林保护区中心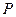 点在
点在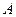 城市的北偏东30°方向,
城市的北偏东30°方向,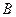 城市的北偏西45°方向上,已知森林保护区的范围在以
城市的北偏西45°方向上,已知森林保护区的范围在以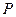 为圆心,50千米为半径的圆形区域内。请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?
为圆心,50千米为半径的圆形区域内。请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?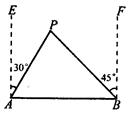
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
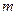 ,
, 上任意两点,C是直线
上任意两点,C是直线 上一点,且
上一点,且 AB (k≠0).
AB (k≠0). =1
=1 时,在图(1)中,作∠BEF=∠ABC,EF交直线
时,在图(1)中,作∠BEF=∠ABC,EF交直线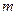 于点F.,写出线段EF与
于点F.,写出线段EF与 ≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 气球与高楼的水平距离为60 m,这栋高楼有多高?(结果精确到0. 1 m,参考数据:sin50°≈0.78,cos50°≈0.
气球与高楼的水平距离为60 m,这栋高楼有多高?(结果精确到0. 1 m,参考数据:sin50°≈0.78,cos50°≈0. 64 ,tan50°≈1.19 ,
64 ,tan50°≈1.19 ,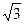 ≈1.73 )
≈1.73 )
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.6sin15°cm | B.6cos15°cm | C.6tan15° cm | D.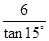 cm cm |
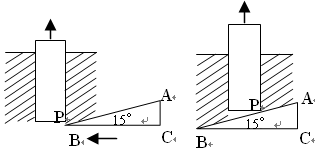
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com