
”¾ĢāÄæ”æŅŃÖŖŹ½×Ó ![]() ŹĒ¹ŲÓŚxµÄ¶ž“Ī¶ąĻīŹ½£¬ĒŅ¶ž“ĪĻīĻµŹżĪŖb£¬ŹżÖįÉĻA”¢BĮ½µćĖł¶ŌÓ¦µÄŹż·Ö±šŹĒaŗĶb£®
ŹĒ¹ŲÓŚxµÄ¶ž“Ī¶ąĻīŹ½£¬ĒŅ¶ž“ĪĻīĻµŹżĪŖb£¬ŹżÖįÉĻA”¢BĮ½µćĖł¶ŌÓ¦µÄŹż·Ö±šŹĒaŗĶb£®

(1)Ōņa=____£¬b=____£®A”¢BĮ½µćÖ®¼äµÄ¾ąĄė£ŗ____£»
(2)ÓŠŅ»¶ÆµćP“ÓµćA³ö·¢µŚŅ»“ĪĻņ×óŌĖ¶Æ1øöµ„Ī»³¤¶Č£¬Č»ŗóŌŚŠĀµÄĪ»ÖƵŚ¶ž“ĪŌĖ¶Æ£¬ĻņÓŅŌĖ¶Æ2øöµ„Ī»³¤¶Č£¬ŌŚ“ĖĪ»ÖƵŚČż“ĪŌĖ¶Æ£¬Ļņ×óŌĖ¶Æ3øöµ„Ī»³¤¶Č”°“ÕÕČē“Ė¹ęĀɲ»¶ĻµŲ×óÓŅŌĖ¶Æ£¬µ±ŌĖ¶Æµ½2019“ĪŹ±£¬ĒóµćPĖł¶ŌÓ¦µÄÓŠĄķŹż£®
(3)ŌŚ(2)µÄĢõ¼žĻĀ£¬µćP»į²»»įŌŚÄ³“ĪŌĖ¶ÆŹ±Ē”ŗƵ½“ļijŅ»øöĪ»ÖĆ£¬Ź¹µćPµ½µćBµÄ¾ąĮćĄėŹĒµćPµ½µćAµÄ¾ąĄėµÄ3±¶£æČōæÉÄÜĒėĒó³ö“ĖŹ±µćPµÄĪ»ÖĆ£¬Čō²»æÉÄÜĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©-4£»8£»12£»£Ø2£©-1041£»£Ø3£©“ęŌŚµćP£¬Ź¹µćPµ½µćBµÄ¾ąĮćĄėŹĒµćPµ½µćAµÄ¾ąĄėµÄ3±¶£»µćPĖł¶ŌÓ¦µÄÓŠĄķŹż·Ö±šŹĒ-10ŗĶ-1.
”¾½āĪö”æ
£Ø1£©øł¾Ż¶ž“Ī¶ąĻīŹ½µÄ¶ØŅåµĆ³ö![]() £¬ÓÉ“ĖµĆ³öaµÄÖµ£¬Č»ŗóÓɶąĻīŹ½µÄĻµŹżµÄ¶ØŅåµĆµ½bµÄÖµ£¬ŌņŅ×ĒóĻ߶ĪABµÄÖµ£»
£¬ÓÉ“ĖµĆ³öaµÄÖµ£¬Č»ŗóÓɶąĻīŹ½µÄĻµŹżµÄ¶ØŅåµĆµ½bµÄÖµ£¬ŌņŅ×ĒóĻ߶ĪABµÄÖµ£»
£Ø2£©øł¾ŻĢāŅāµĆµ½µćPĆæŅ»“ĪŌĖ¶ÆŗóĖłŌŚµÄĪ»ÖĆ£¬Č»ŗóÓÉÓŠĄķŹżµÄ¼Ó·Ø½ųŠŠ¼ĘĖć¼“æÉ£»
£Ø3£©ÉčµćP¶ŌÓ¦µÄÓŠĄķŹżµÄÖµĪŖx£¬·ÖĒéæö½ųŠŠ½ā“š£ŗµćPŌŚµćAµÄ×ó²ą£¬µćPŌŚµćA”¢BÖ®¼ä£¬µćPŌŚµćBµÄÓŅ²ąČżÖÖĒéæö.
£Ø1£©”ß![]() ŹĒ¹ŲÓŚxµÄ¶ž“Ī¶ąĻīŹ½£¬ĒŅ¶ž“ĪĻīĻµŹżĪŖb£¬
ŹĒ¹ŲÓŚxµÄ¶ž“Ī¶ąĻīŹ½£¬ĒŅ¶ž“ĪĻīĻµŹżĪŖb£¬
”ą![]()
Ōņ![]()
”ąA”¢BĮ½µćÖ®¼äµÄ¾ąĄėĪŖ![]()
¹Ź“š°øĪŖ-4£»8£»12
£Ø2£©ŅĄĢāŅāµĆ£¬-4-1+2-3+4-5+6-7+””+2018-2019
=-4+1009-2019
=-1041
¹ŹµćPĖł¶ŌÓ¦µÄÓŠĄķŹżµÄÖµĪŖ-1041.
£Ø3£©ÉčµćP¶ŌÓ¦µÄÓŠĄķŹżµÄÖµĪŖx
¢Łµ±µćPŌŚµćAµÄ×ó²ąŹ±£¬
PA=-4-x£¬PB=8-x
ŅĄĢāŅāµĆ£¬8-x=3£Ø-4-x£©
½āµĆx=-10£»
¢Śµ±µćPŌŚµćAŗĶµćBÖ®¼äŹ±£¬
PA=x-£Ø-4£©=x+4,PB=8-x
ŅĄĢāŅāµĆ£¬8-x=3(x+4)
½āµĆx=-1£»
¢Ūµ±µćPŌŚµćBµÄÓŅ²ąŹ±£¬
PA=x-£Ø-4£©=x+4£¬PB=x-8
ŅĄĢāŅāµĆ£¬x-8=3£Øx+4£©
½āµĆx=-10,ÕāÓėµćPŌŚµćBµÄÓŅ²ą£Ø¼“x£¾8£©Ć¬¶Ü£¬¹ŹÉįČ„£»
×ŪÉĻĖłŹö£¬µćPĖł¶ŌÓ¦µÄÓŠĄķŹż·Ö±šŹĒ-10ŗĶ-1.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涞“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄ²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬Ę䶄µć×ų±źĪŖ£Ø1£¬n£©£¬ĒŅÓėxÖįµÄŅ»øö½»µćŌŚ£Ø3£¬0£©ŗĶ£Ø4£¬0£©Ö®¼ä£¬ŌņĻĀĮŠ½įĀŪ£ŗ
¢Łac![]()
¢Śa©b+c£¾0£»
¢Ūµ±![]() Ź±£¬yĖęxµÄŌö“ó¶ųŌö“ó
Ź±£¬yĖęxµÄŌö“ó¶ųŌö“ó
Čō£Ø©![]() £¬y1£©£¬£Ø
£¬y1£©£¬£Ø![]() £¬y2£©ŹĒÅ×ĪļĻßÉĻµÄĮ½µć£¬Ōņy1
£¬y2£©ŹĒÅ×ĪļĻßÉĻµÄĮ½µć£¬Ōņy1![]() y2£»
y2£»
¢ÜŅ»ŌŖ¶ž“Ī·½³Ģax2+bx+c=n©1ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£®
ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø””””£©
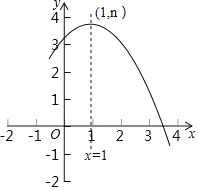
A. 1 B. 2 C. 3 D. 4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µć![]() µÄ×ų±źĪŖ£Ø
µÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£¬µć
£©£¬µć![]() ŹĒ
ŹĒ![]() ÖįÕż°ėÖįÉĻµÄŅ»¶Æµć£¬ŅŌ
ÖįÕż°ėÖįÉĻµÄŅ»¶Æµć£¬ŅŌ![]() ĪŖ±ß×÷µČŃüÖ±½Ē
ĪŖ±ß×÷µČŃüÖ±½Ē![]() £¬Ź¹
£¬Ź¹![]() £¬Éčµć
£¬Éčµć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬µć
£¬µć![]() µÄׯ×ų±źĪŖ
µÄׯ×ų±źĪŖ![]() £¬ÄܱķŹ¾
£¬ÄܱķŹ¾![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµµÄĶ¼Ļó“óÖĀŹĒ
µÄŗÆŹż¹ŲĻµµÄĶ¼Ļó“óÖĀŹĒ
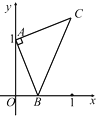
A. 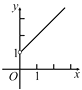 B.
B. 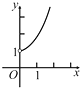 C.
C.  D.
D. 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø±¾Ģā9·Ö£©¾Ż±ØµĄ£¬”°¹ś¼Ź¼ōµ¶ŹÆĶ·²¼Š»į”±ĢįŅ齫”°¼ōµ¶ŹÆĶ·²¼”±×÷ĪŖ°ĀŌĖ»į±ČČüĻīÄ森ijŠ£Ń§Éś»įĻėÖŖµĄŃ§Éś¶ŌÕāøöĢįŅéµÄĮĖ½ā³Ģ¶Č£¬Ė껜³éČ”²æ·Öѧɜ½ųŠŠĮĖŅ»“ĪĪŹ¾ķµ÷²é£¬²¢øł¾ŻŹÕ¼Æµ½µÄŠÅĻ¢½ųŠŠĮĖĶ³¼Ę£¬»ęÖĘĮĖĻĀĆęĮ½·łÉŠ²»ĶźÕūµÄĶ³¼ĘĶ¼£®ĒėÄćøł¾ŻĶ³¼ĘĶ¼ÖŠĖłĢį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
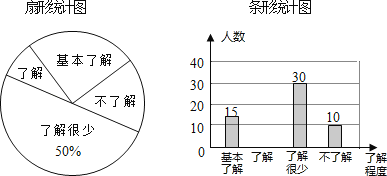
£Ø1£©½ÓŹÜĪŹ¾ķµ÷²éµÄѧɜ¹²ÓŠ___Ćū£¬ÉČŠĪĶ³¼ĘĶ¼ÖŠ”°»ł±¾ĮĖ½ā”±²æ·ÖĖł¶ŌÓ¦ÉČŠĪµÄŌ²ŠÄ½ĒĪŖ___£»Ēė²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø2£©ČōøĆŠ£¹²ÓŠŃ§Éś900ČĖ£¬Ēėøł¾ŻÉĻŹöµ÷²é½į¹ū£¬¹Ą¼ĘøĆŠ£Ń§ÉśÖŠ¶Ō½«”°¼ōµ¶ŹÆĶ·²¼”±×÷ĪŖ°ĀŌĖ»į±ČČüĻīÄæµÄĢįŅé“ļµ½”°ĮĖ½ā”±ŗĶ”°»ł±¾ĮĖ½ā”±³Ģ¶ČµÄ×ÜČĖŹż£»
£Ø3£©”°¼ōµ¶ŹÆĶ·²¼”±±ČČüŹ±Ė«·½Ćæ“ĪČĪŅā³ö”°¼ōµ¶”±”¢”°ŹÆĶ·”±”¢”°²¼”±ÕāČżÖÖŹÖŹĘÖŠµÄŅ»ÖÖ£¬¹ęŌņĪŖ£ŗ¼ōµ¶Ź¤²¼£¬²¼Ź¤ŹÆĶ·£¬ŹÆĶ·Ź¤¼ōµ¶£¬ČōĖ«·½³öĻÖĻąĶ¬ŹÖŹĘ£¬ŌņĖć“ņĘ½£®ČōŠ”øÕŗĶŠ”Ć÷Į½ČĖÖ»±ČČüŅ»¾Ö£¬ĒėÓĆŹ÷דĶ¼»ņĮŠ±ķ·ØĒóĮ½ČĖ“ņĘ½µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
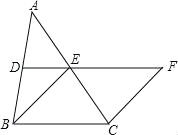
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬D”¢E·Ö±šŹĒAB”¢ACµÄÖŠµć£¬BE£½2DE£¬ŃÓ³¤DEµ½µćF£¬Ź¹µĆEF£½BE£¬Į¬½ÓCF£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪBCFEŹĒĮāŠĪ£»
£Ø2£©ČōCE£½2£¬”ĻBCF£½120”ć£¬ĒóĮāŠĪBCFEµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚÕż·½ŠĪABCDÖŠ£¬EŹĒBC±ßÉĻŅ»µć£¬FŹĒBAŃÓ³¤ĻßÉĻŅ»µć£¬AF£½CE£¬Į¬½ÓBD£¬EF£¬FGĘ½·Ö”ĻBFE½»BDÓŚµćG£®
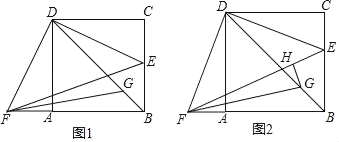
£Ø1£©ĒóÖ¤£ŗ”÷ADF”Õ”÷CDE£»
£Ø2£©ĒóÖ¤£ŗDF£½DG£»
£Ø3£©ČēĶ¼2£¬ČōGH”ĶEFÓŚµćH£¬ĒŅEH£½![]() FH£¬ÉčÕż·½ŠĪABCDµÄ±ß³¤ĪŖx£¬GH£½y£¬ĒóyÓėxÖ®¼äµÄ¹ŲĻµŹ½£®
FH£¬ÉčÕż·½ŠĪABCDµÄ±ß³¤ĪŖx£¬GH£½y£¬ĒóyÓėxÖ®¼äµÄ¹ŲĻµŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬DĪŖ”ŃOÉĻŅ»µć£¬µćCŌŚÖ±¾¶BAµÄŃÓ³¤ĻßÉĻ£¬ĒŅ”ĻCDA=”ĻCBD£®
£Ø1£©ĒóÖ¤£ŗCDŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©¹żµćB×÷”ŃOµÄĒŠĻß½»CDµÄŃÓ³¤ĻßÓŚµćE£¬BC=6£¬ ![]() £®ĒóBEµÄ³¤£®
£®ĒóBEµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”放ĪŹĢā·¢ĻÖ”æ
£Ø1£©ČēĶ¼£Ø1£©£¬ĖıߊĪABCDÖŠ£¬ČōAB=AD£¬CB=CD£¬ŌņĻ߶ĪBD£¬ACµÄĪ»ÖĆ¹ŲĻµĪŖ__________£»
”¾ĶŲÕ¹Ģ½¾æ”æ
£Ø2£©ČēĶ¼£Ø2£©£¬ŌŚRt”÷ABCÖŠ£¬µćFĪŖŠ±±ßBCµÄÖŠµć£¬·Ö±šŅŌAB£¬ACĪŖµ×±ß£¬ŌŚRt”÷ABCĶā²æ×÷µČŃüČż½ĒŠĪABDŗĶµČŃüČż½ĒŠĪACE£¬Į¬½ÓFD£¬FE£¬·Ö±š½»AB£¬ACÓŚµćM£¬N£®ŹŌ²ĀĻėĖıߊĪFMANµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
”¾½ā¾öĪŹĢā”æ
£Ø3£©ČēĶ¼£Ø3£©£¬ŌŚÕż·½ŠĪABCDÖŠ£¬AB=2![]() £¬ŅŌµćAĪŖŠż×ŖÖŠŠÄ½«Õż·½ŠĪABCDŠż×Ŗ60”ć£¬µĆµ½Õż·½ŠĪAB'C'D'£¬ĒėÖ±½ÓŠ“³öBD'Ę½·½µÄÖµ£®
£¬ŅŌµćAĪŖŠż×ŖÖŠŠÄ½«Õż·½ŠĪABCDŠż×Ŗ60”ć£¬µĆµ½Õż·½ŠĪAB'C'D'£¬ĒėÖ±½ÓŠ“³öBD'Ę½·½µÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢµź¾ĻśŅ»ÖÖĖ«¼ē°ü£¬ŅŃÖŖÕāÖÖĖ«¼ē°üµÄ³É±¾¼ŪĪŖĆæøö30ŌŖ£®ŹŠ³”µ÷²é·¢ĻÖ£¬ÕāÖÖĖ«¼ē°üĆæĢģµÄĻśŹŪĮæy£Øµ„Ī»:øö£©ÓėĻśŹŪµ„¼Ūx£Øµ„Ī»:ŌŖ£©ÓŠČēĻĀ¹ŲĻµ£ŗy=£x+60£Ø30”Üx”Ü60£©£®
ÉčÕāÖÖĖ«¼ē°üĆæĢģµÄĻśŹŪĄūČóĪŖwŌŖ£®
£Ø1£©ĒówÓėxÖ®¼äµÄŗÆŹż½āĪöŹ½£»
£Ø2£©ÕāÖÖĖ«¼ē°üĻśŹŪµ„¼Ū¶ØĪŖ¶ąÉŁŌŖŹ±£¬ĆæĢģµÄĻśŹŪĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁŌŖ£æ
£Ø3£©Čē¹ūĪļ¼Ū²æĆŹę¶ØÕāÖÖĖ«¼ē°üµÄĻśŹŪµ„¼Ū²»øßÓŚ48ŌŖ£¬øĆÉĢµźĻśŹŪÕāÖÖĖ«¼ē°üĆæĢģŅŖ»ńµĆ200ŌŖµÄĻśŹŪĄūČó£¬ĻśŹŪµ„¼ŪÓ¦¶ØĪŖ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com