
分析 以点B为圆心线段AB长为半径做圆,交抛物线于点C、M、N点,连接AC、BC,由直线y=-$\sqrt{3}$x+3可求出点A、B的坐标,结合抛物线的解析式可得出△ABC等边三角形,再令抛物线解析式中y=0求出抛物线与x轴的两交点的坐标,发现该两点与M、N重合,结合图形分三种情况研究△ABP为等腰三角形,由此即可得出结论.
解答 解:以点B为圆心线段AB长为半径做圆,交抛物线于点C、M、N点,连接AC、BC,如图所示.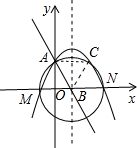
令一次函数y=-$\sqrt{3}$x+3中x=0,则y=3,
∴点A的坐标为(0,3);
令一次函数y=-$\sqrt{3}$x+3中y=0,则-$\sqrt{3}$x+3=0,
解得:x=$\sqrt{3}$,
∴点B的坐标为($\sqrt{3}$,0).
∴AB=2$\sqrt{3}$.
∵抛物线的对称轴为x=$\sqrt{3}$,
∴点C的坐标为(2$\sqrt{3}$,3),
∴AC=2$\sqrt{3}$=AB=BC,
∴△ABC为等边三角形.
令y=-$\frac{1}{3}$(x-$\sqrt{3}$)2+4中y=0,则-$\frac{1}{3}$(x-$\sqrt{3}$)2+4=0,
解得:x=-$\sqrt{3}$,或x=3$\sqrt{3}$.
∴点E的坐标为(-$\sqrt{3}$,0),点F的坐标为(3$\sqrt{3}$,0).
△ABP为等腰三角形分三种情况:
①当AB=BP时,以B点为圆心,AB长度为半径做圆,与抛物线交于C、M、N三点;
②当AB=AP时,以A点为圆心,AB长度为半径做圆,与抛物线交于C、M两点,;
③当AP=BP时,作线段AB的垂直平分线,交抛物线交于C、M两点;
∴能使△ABP为等腰三角形的点P的个数有3个.
故答案为:3.
点评 本题考查了二次函数与坐标轴的交点坐标、等腰三角形的判定、一次函数与坐标轴的交点坐标以及等边三角形的判定定理,解题的关键是依照题意画出图形,利用数形结合来解决问题.本题属于中档题,难度不小,本题不需要求出P点坐标,但在寻找点P的过程中会出现多次点的重合问题,由此给解题带来了难度.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:选择题
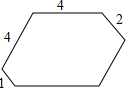 如图,一个六边形的六个内角都是120°,其连续四条边的长依次为1,4,4,2;那么这个六边形的周长是( )
如图,一个六边形的六个内角都是120°,其连续四条边的长依次为1,4,4,2;那么这个六边形的周长是( )| A. | 19 | B. | 20 | C. | 25 | D. | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+2y=1 | B. | 2y+$\frac{y}{2}$+1=0 | C. | $\frac{2}{x}$+3=0 | D. | 2y2=8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).
已知:关于x的一元二次方程ax2-2(a-1)x+a-2=0(a>0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
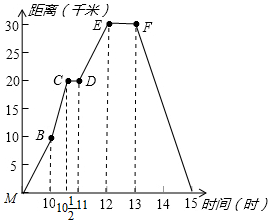 如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题:
如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com