
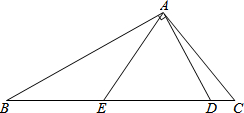
 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.分析 (1)首先利用直角三角形斜边上的中线等于斜边的一半可得AE=BE=ED,再根据等边对等角可得∠B=∠BAE,从而可得∠AEC=∠B+∠BAE=2∠B,再由条件∠C=2∠B可得结论;
(2)首先利用勾股定理计算出2AB的长,然后可得答案.
解答 (1)证明:∵AD⊥AB,
∴△ABD为直角三角形,
又∵点E是BD的中点,
∴$AE=\frac{1}{2}BD=BE$,
∴∠B=∠BAE,∠AEC=∠B+∠BAE=2∠B,
又∵∠C=2∠B,
∴∠AEC=∠C;
(2)解:在Rt△ABD中,AD=5,BD=2AE=2×6.5=13,
∴$AB=\sqrt{B{D^2}-A{D^2}}=\sqrt{{{13}^2}-{5^2}}=12$,
∴△ABE的周长=AB+BE+AE=12+6.5+6.5=25.
点评 此题主要考查了勾股定理,以及直角三角形的性质,关键是掌握在直角三角形中,斜边上的中线等于斜边的一半.


科目:初中数学 来源: 题型:选择题
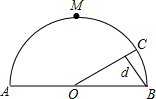 如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )
如图是自行车骑行训练场地的一部分,半圆O的直径AB=100,在半圆弧上有一运动员C从B点沿半圆周匀速运动到M(最高点),此时由于自行车故障原地停留了一段时间,修理好继续以相同的速度运动到A点停止.设运动时间为t,点B到直线OC的距离为d,则下列图象能大致刻画d与t之间的关系是( )| A. | 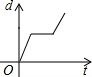 | B. | 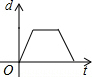 | C. | 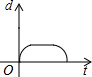 | D. | 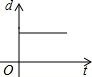 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
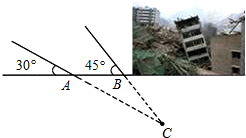 2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
2015年4月25日14时11分,尼泊尔发生8.1级地震,震源深度20千米.中国救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧某面上选两探测点A、B,AB相距2米,探测线与该面的夹角分别是30°和45°(如图).试确定生命所在点C与探测面的距离.(参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥$\frac{1}{2}$ | B. | x≤1 | C. | $\frac{1}{2}$≤x≤1 | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这组数据的平均数是75 | B. | 这组数据的中位数是74 | ||
| C. | 这组数据的方差是3.2 | D. | 这组数据的众数是76 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com