
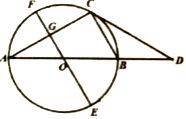
【题目】如图,⊙O是△ABC的外接圆,AB为⊙O的直径,过点C作∠BCD=∠CAB交AB的延长线于点D,过点O作直径EF∥BC,交AC于点G.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为2,∠BCD=30°.
①连接AE、DE,求证:四边形ACDE是菱形.
②当点P是线段AD上的一动点时,求PF+PG的最小值.
【答案】(1)见解析;(2)①见解析,②PF+PG的最小值为![]() .
.
【解析】
(1)连接OC,由AB是直径可得∠ACB=90°,由OC=OB可得∠ABC=∠OCB,由锐角互余的关系可得![]() ,即可得答案;(2)①连线AE、ED、BE,由∠BCD=30°,可得∠OCB=60°,进而可得∠OBC=60°,根据外角性质可得∠CDA=30°,即可证明∠CDA=∠CAD,可得AC=DC,由平行线性质可得
,即可得答案;(2)①连线AE、ED、BE,由∠BCD=30°,可得∠OCB=60°,进而可得∠OBC=60°,根据外角性质可得∠CDA=30°,即可证明∠CDA=∠CAD,可得AC=DC,由平行线性质可得![]() ,进而可得
,进而可得![]() ,即可证明ΔOCB,ΔOEB是等边三角形,易证明
,即可证明ΔOCB,ΔOEB是等边三角形,易证明![]() ,
,![]() ,可得AC=CD=AE=ED即可得答案;②作F关于直线AB的对称点H,H在⊙O上,连接GH交AB于P点,此时线段GH最短,则PF+PG最小,连接OH,过H作HI⊥EF,可求出
,可得AC=CD=AE=ED即可得答案;②作F关于直线AB的对称点H,H在⊙O上,连接GH交AB于P点,此时线段GH最短,则PF+PG最小,连接OH,过H作HI⊥EF,可求出![]() ,
,![]() ,在Rt△AGO中,利用三角函数可求出OG的长,在Rt△HIO中可求出OI、HI的长,利用勾股定理求出GH的长即可.
,在Rt△AGO中,利用三角函数可求出OG的长,在Rt△HIO中可求出OI、HI的长,利用勾股定理求出GH的长即可.
(1)连接OC,
∵OC=OB,
∴![]() ,
,
∵AB是⊙O的直径,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴OC⊥CD,
∴CD是⊙O切线.
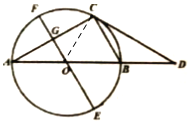
(2)①连线AE、ED、BE,
∵![]()
∴![]()
∴![]()
∴AC=DC
∵EF∥BC
∴![]()
∴![]()
∵OE=OB=BE
∴ΔOCB,ΔOEB是等边三角形
∵BC=OB=BE
∴易证![]() ,
,![]()
∴AC=CD=AE=ED
∴四边形ACDE是菱形,
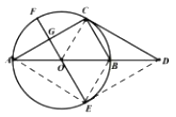
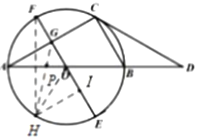
②作F关于直线AB的对称点H,H在⊙O上,连接GH交AB于P点,此时线段GH最短,则PF+PG最小,连接OH,过H作HI⊥EF
由①已证![]()
又∵F于H关于直线AB对称
∴![]()
∴![]() ,
,![]()
在RtΔAGO中,OA=2
∴![]()
在RtΔHIO中,OH=2
∴![]() ,
,![]()
∴![]()
∴PF+PG的最小值为![]()


科目:初中数学 来源: 题型:
【题目】某校为了了解全校400名学生参加课外锻炼的情况,随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查,结果如下:(单位:分)
40 21 35 24 40 38 23 52 35 62
36 15 51 45 40 42 40 32 43 36
34 53 38 40 39 32 45 40 50 45
40 40 26 45 40 45 35 40 42 45
(1)补全频率分布表和频率分布直方图.
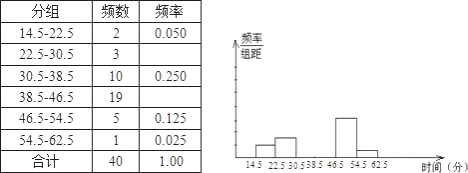
(2)填空:在这个问题中,总体是_____,样本是_____.由统计结果分析的,这组数据的平均数是38.35(分),众数是_____,中位数是______.
(3)如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况,你认为用平均数、众数、中位数中的哪一个量比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如下不完整统计图.
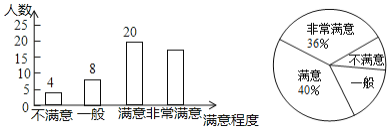
请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为多少人,其中“非常满意”的人数为多少人;
(2)兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访,已知这4位群众中有2位来自甲片区,另2位来自乙片区,请用画树状图或列表的方法求出选择的群众来自甲片区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝即将到来的“三月三”壮族传统节日,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成如下图表:
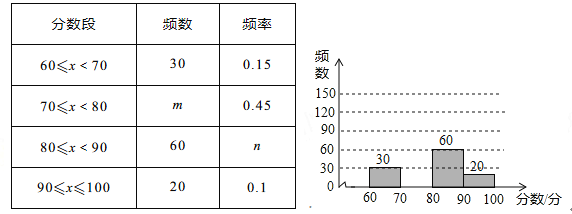
请根据如上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生,表中的数![]() .
.![]() .
.
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段![]() 所对应扇形的圆心角为 度;
所对应扇形的圆心角为 度;
(4)全校共有![]() 名学生参加比赛,估计该校成绩
名学生参加比赛,估计该校成绩![]() 范围内的学生有多少人?
范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的分式方程![]() 的解为正数,使关于y的不等式组
的解为正数,使关于y的不等式组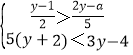 无解,则所有满足条件的整数a的值之积是( )
无解,则所有满足条件的整数a的值之积是( )
A. 360 B. 90 C. 60 D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
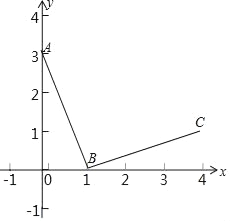
【题目】如图,在平面直角坐标系xOy中,A(0,3),B(1,0),连接BA,将线段BA绕点B顺时针旋转90°得到线段BC,反比例函数y=![]() 的图象G经过点C.
的图象G经过点C.
(1)请直接写出点C的坐标及k的值;
(2)若点P在图象G上,且∠POB=∠BAO,求点P的坐标;
(3)在(2)的条件下,若Q(0,m)为y轴正半轴上一点,过点Q作x轴的平行线与图象G交于点M,与直线OP交于点N,若点M在点N左侧,结合图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
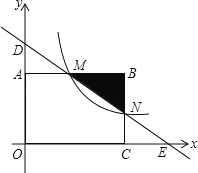
【题目】如图,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,B(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)直接写出直线DE的解析式_________;
(2)若反比例函数y=![]() (x>0)的图象与直线MN有且只有一个公共点,求m的值.
(x>0)的图象与直线MN有且只有一个公共点,求m的值.
(3)在分别过M,B的双曲线y=![]() (x>0)上是否分别存在点F,G使得B,M,F,G构成平行四边形,若存在则求出F点坐标, 若不存在则说明理由.
(x>0)上是否分别存在点F,G使得B,M,F,G构成平行四边形,若存在则求出F点坐标, 若不存在则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com