
【题目】在平面直角坐标系xOy中,点P的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,且
,且![]() ,
,![]() ,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.
,若P,Q为某正方形的两个顶点,且该正方形的边均与某条坐标轴平行(含重合),则称P,Q互为“正方形点”(即点P是点Q的“正方形点”,点Q也是点P的“正方形点”).下图是点P,Q互为“正方形点”的示意图.

已知点A的坐标是(2,3),下列坐标中,与点A互为“正方形点”的坐标是____________.(填序号)
①(1,2);②(-1,5);③(3,2).
(2)若点B(1,2)的“正方形点”C在y轴上,求直线BC的表达式;
(3)点D的坐标为(-1,0),点M的坐标为(2,m),点N是线段OD上一动点(含端点),若点M,N互为“正方形点”,求m的取值范围.
【答案】(1) ①③;(2) ![]() 或
或 ![]() ;(3)
;(3) ![]() 或
或![]() .
.
【解析】(1)根据点A互为“正方形点”的坐标定义即可求出所求的坐标;(2)由已知条件先求出点C的坐标,利用待定系数法求得直线BC的表达式;(3)由点N是线段OD上一动点(含端点),求出点D、O的正方形点坐标,结合图象写出m的取值范围.
解:(1)①③
(2)∵点B(1,2)的“正方形点”C在y轴上,
∴点C的坐标为(0,1),(0,3),
∴直线BC的表达式为![]() ,
,![]() .
.
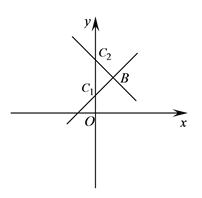
(3)过点OD分别作与x轴夹角为![]() 的直线,
的直线,
∵点M的坐标为(2,m),点N是线段OD上一动点(含端点),
点M,N互为“正方形点”,
∴点D的正方形点坐标是(2,3),(2,-3),
点O的正方形点坐标是(2,2),(2,-2),
∴![]() 或
或![]() .
.

“点睛”本题考查了新定义问题,涉及到一次函数的知识,解题时要理解“正方形点”的定义,对学生的综合能力要求即较高,一定要注意将新知识贯穿整个解题中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】用计算器求下列三角函数(保留四位小数):sin38°19′=________;cos78°43′16″=________;tan57°26′=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖北襄阳第18题)
襄阳市文化底蕴深厚,旅游资源丰富,古隆中、习家池、鹿门寺三个景区是人们节假日游玩的热点景区.张老师对八(1)班学生“五·一”小长假随父母到这三个景区游玩的计划做了全面调查,凋奄分四个类别:A游三个景区; B游两个景区;C游一个景区;D不到这三个景区游玩.现根据调查结果绘制了不完整饷条形统计图和扇形统计图,请结合图中信息解答下列问题.
(1)八(1)班共有学生 人,在扇形统计图中,表示“B 类别”的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整:
(3)若张华、李刚两名同学,各自从三个景区中随机选一个作为5月1日游玩的景区,则他们同时选中古隆中的概率为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面的材料,完成有关问题.
材料:在学习绝对值时,老师教过我们绝对值的几何含义,如|5﹣3|表示5、3在数轴上对应的两点之间的距离;|5+3|=|5﹣(﹣3)|,所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离;|5|=|5﹣0|,所以|5|表示5在数轴上对应的点到原点的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
问题(1):点A、B、C在数轴上分别表示有理数﹣5、﹣1、3,那么A到B的距离是 ,
A到C的距离是 . (直接填最后结果).
问题(2):点A、B、C在数轴上分别表示有理数x、﹣2、1,那么A到B的距离与A到C的距离之和可表示为 (用含绝对值的式子表示).
问题(3):利用数轴探究:①找出满足|x﹣3|+|x+1|=6的x的所有值是 ;
②设|x﹣3|+|x+1|=p,当x的值取在不小于﹣1且不大于3的范围时,p的值是不变的,而且是p的最小值,这个最小值是 ;当x的值取在 的范围时,|x|+|x﹣2|的最小值是 .
问题(4):求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a=-2×32,b=(-2×3)2,c=-(2×3)2,那么a,b,c的大小关系是( )
A. a<c<b B. a<b<c C. c<a<b D. c<b<a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣![]() x+
x+![]() 与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
(1)求抛物线m的解析式;
(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;
(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com