

分析 (1)根据阴影部分的面积=4个小长方形的面积=大正方形的面积-小正方形的面积,利用完全平方公式,即可解答;
(2)根据完全平方公式解答;
(3)根据平方差公式解答.
解答 解:(1)阴影部分的面积为:4ab或(a+b)2-(a-b)2,
得到等式:4ab=(a+b)2-(a-b)2;
(2)右边=a2+2ab+b2-(a2-2ab+b2)=a2+2ab+b2-a2+2ab-b2=4ab=左边,即等式成立;
(3)(2m+n)2-(2m-n)2=4×2mn,
13-5=8mn,
mn=1.
点评 本题考查了完全平方公式的几何背景,准确识图,根据阴影部分的面积的两种不同表示方法得到的代数式的值相等列式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上一动点(不与B,C重合),E是AC上一个动点,始终保持∠ADE=∠B,则当△DCE为直角三角形时,BD的长为4或$\frac{25}{4}$.
如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上一动点(不与B,C重合),E是AC上一个动点,始终保持∠ADE=∠B,则当△DCE为直角三角形时,BD的长为4或$\frac{25}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A、P在反比例函数y=$\frac{k}{x}$(k<0)的图象上,点B、Q在直线y=x-3的图象上,点B的纵坐标为-1,AB⊥x轴,且S△OAB=4.若P、Q两点关于y轴对称,设点P的坐标为(m,n).
如图,已知点A、P在反比例函数y=$\frac{k}{x}$(k<0)的图象上,点B、Q在直线y=x-3的图象上,点B的纵坐标为-1,AB⊥x轴,且S△OAB=4.若P、Q两点关于y轴对称,设点P的坐标为(m,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,∠C=90°,AC<BC.D为BC上一点,且到A、B两点的距离相等.
如图,已知△ABC中,∠C=90°,AC<BC.D为BC上一点,且到A、B两点的距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
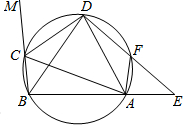 如图,在圆内接四边形ABCD中,CD为∠BAC的外角平分线,F为$\widehat{AD}$上一点,BC=AF,延长DF与BA的延长线交于E.
如图,在圆内接四边形ABCD中,CD为∠BAC的外角平分线,F为$\widehat{AD}$上一点,BC=AF,延长DF与BA的延长线交于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.取AB边的中点F,连接CF、CE,试判断四边形AFCE的形状.并说明理由.
如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.取AB边的中点F,连接CF、CE,试判断四边形AFCE的形状.并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com