
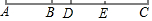 如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB.
如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB.分析 (1)根据线段间的关系,可得BC的长,根据线段的和差,可得答案;
(2)①根据线段间的关系,可得关于AD的方程,根据解方程,可得答案;
②根据线段中点的性质,可得BE的长,根据线段的和差,可得答案.
解答 解:(1)由AB=3cm,延长线段AB到C,使BC=2AB,得
BC=2AB=6cm,
由线段的和差,得
AC=AB+BC=3+6=9cm,
故答案为:9cm;
(2)①由AD比DC短1cm,得
DC=AD+1.
由线段的和差,得
DC+AD=9,即AD+AD+1=9,
解得AD=4cm,
线段AD的长是4cm;
②由点E是BC的中点,BC=6cm,得
BE=$\frac{1}{2}$BC=3cm.
由线段的和差,得
AE=AB+BE=3=3=6cm,
DE=AE-AD=6-4=2cm,
线段DE的长是2cm.
点评 本题考查了两点间的距离,利用线段中点的性质,线段的和差是解题关键.


科目:初中数学 来源: 题型:解答题
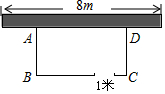 有一个面积为30平方米的长方形ABCD的鸡场,鸡场的一边靠墙(墙长8米),墙的对面有一个1米宽的门,另三边用竹篱笆围成,篱笆总长15米,求鸡场的宽AB是多少米?
有一个面积为30平方米的长方形ABCD的鸡场,鸡场的一边靠墙(墙长8米),墙的对面有一个1米宽的门,另三边用竹篱笆围成,篱笆总长15米,求鸡场的宽AB是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
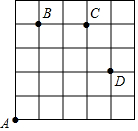 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
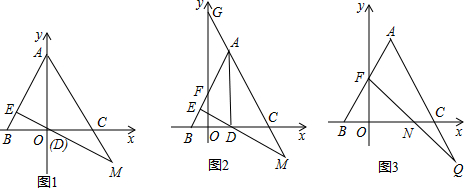
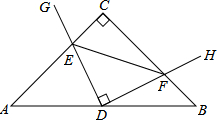 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:| A. | ①②③④ | B. | ①②③ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com