
【题目】已知关于x的一元二次方程x2-2kx+![]() k2-2=0.
k2-2=0.
(1)求证:不论k为何值,方程总有两不相等实数根.
(2)设x1,x2是方程的根,且 x12-2kx1+2x1x2=5,求k的值.
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为边
为边![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一点,联结
上一点,联结![]() 并延长交边
并延长交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平分线,交射线
的平分线,交射线![]() 于点
于点![]() .设
.设![]() .
.

(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)设![]() ,求关于
,求关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
(1)求抛物线的函数解析式;
(2)若D是抛物线位于第一象限上的动点,求△BCD面积的最大值及此时点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在CB的延长线上,BA平分∠EBD,AE=AB.
(1)求证:AC=AD.
(2)当![]() ,AD=6时,求CD的长.
,AD=6时,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
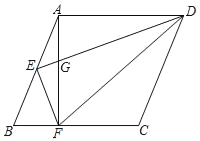
【题目】如图,已知菱形ABCD,点E是AB的中点,AF⊥BC于点F,联结EF、ED、DF,DE交AF于点G,且AE2=EGED.
(1)求证:DE⊥EF;
(2)求证:BC2=2DFBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
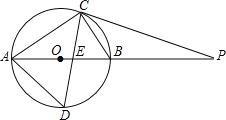
【题目】如图⊙O的直径AB=10cm,弦BC=6cm,∠ACB的平分线交⊙O于D,交AB于E,P是AB延长线上一点,且PC=PE.
(l)求证:PC是⊙O的切线;
(2)求AC、AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如下表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).
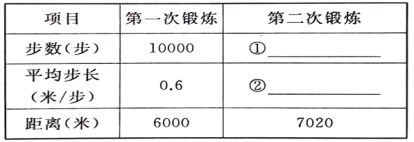
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x的值;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
查看答案和解析>>
科目:初中数学 来源: 题型:
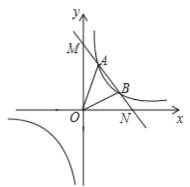
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点A(
的图象交于点A(![]() )、
)、![]() 两点,与坐标轴分别交于M、N两点.
两点,与坐标轴分别交于M、N两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 中
中![]() 的取值范围是____________;
的取值范围是____________;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据![]() )( )
)( )
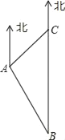
A. 7.3海里B. 10.3海里C. 17.3海里D. 27.3海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com