
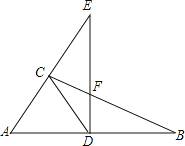
【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有______
,则下列结论正确的有______ ![]() 将所有正确答案的序号都填在横线上
将所有正确答案的序号都填在横线上![]()
![]() ;
;![]() ;
;![]() 是等边三角形;
是等边三角形;![]() 若
若![]() ,则
,则![]() .
.
【答案】![]()
【解析】
由在△ABC中,∠ACB=90°,DE⊥AB,易证得∠DCA=∠DAC,继而可得①∠DCB=∠B正确;
由①可证得AD=BD=CD,即可得②CD=![]() AB正确;
AB正确;
易得③△ADC是等腰三角形,但不能证得△ADC是等边三角形;
由若∠E=30°,易求得∠FDC=∠FCD=30°,则可证得DF=CF,继而证得DE=EF+CF.
∵在△ABC中,∠ACB=90°,DE⊥AB,
∴∠ADE=∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠DCB=90°,
∵∠DCA=∠DAC,
∴AD=CD,∠DCB=∠B;故①正确;
∴CD=BD,
∵AD=BD,
∴CD=![]() AB;故②正确;
AB;故②正确;
∠DCA=∠DAC,
∴AD=CD,
但不能判定△ADC是等边三角形;故③错误;
∵若∠E=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴∠ADC=30°,
∵∠ADE=∠ACB=90°,
∴∠EDC=∠BCD=∠B=30°,
∴CF=DF,
∴DE=EF+DF=EF+CF.故④正确.
故答案为:①②④.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的数阵是由77个偶数排成:
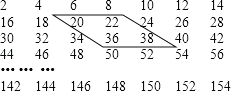
(1)如图中任意作一个平行四边形框,设左上角的数为x,那么其他3个数从小到大可分别表示为 .
(2)小红说这4个数的和是292,能求出这4个数吗?若存在,请求出这4个数.不存在说明理由.
(3)小明说4个数的和是420,存在这样的数吗?若存在,请求出这4个数,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】

(1)请你根据图中A、B两点的位置,分别写出它们所表示的有理数
A: ___________ B: _____________ ;
(2)观察数轴,与点A的距离为4的点表示的数是:_____________ ;
(3)若将数轴折叠,使得A点与-3表示的点重合,则B点与数_ _表示的点重合;
(4)若数轴上M、N两点之间的距离为2014(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是: M: _______ N: _______.
查看答案和解析>>
科目:初中数学 来源: 题型:
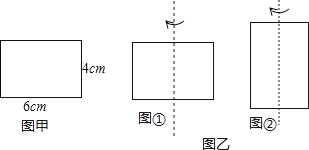
【题目】探究:有一长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是 . 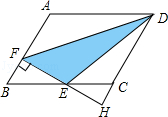
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC. 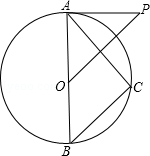
(1)求证:PA为⊙O的切线;
(2)若OB=5,OP= ![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com