
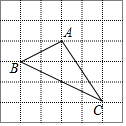
 如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$.
如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$. 分析 利用△ABC所在的长方形的面积减去四周三个直角三角形的面积,列式计算即可得解;先根据勾股定理可求AB,AC,BC的长,再把它们相加可求三角形的周长.
解答 解:△ABC的面积=4×3-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×4
=12-1-3-4
=4;
由勾股定理得AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
则△ABC的周长是$\sqrt{5}$+$\sqrt{13}$+2$\sqrt{5}$=3$\sqrt{5}$+$\sqrt{13}$.
故答案为:4;3$\sqrt{5}$+$\sqrt{13}$.
点评 本题考查了勾股定理,三角形的面积的计算,熟练掌握网格结构,根据勾股定理求AB,AC,BC的长是解题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
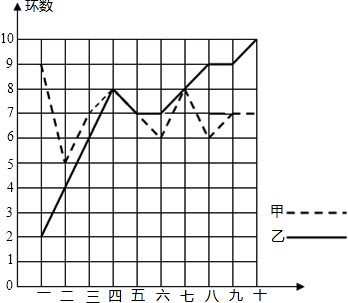 某市射击队甲、乙两名优秀队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
某市射击队甲、乙两名优秀队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:| 平均数 | 方差 | 中位数 | 命中9环(含9环) 以上的环数 | |
| 甲 | 7 | 7 | 1 | |
| 乙 | 5.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知Rt△ABC中,∠B=90°,且AB=2BC,请在图中按如下要求进行操作和证明:
如图,已知Rt△ABC中,∠B=90°,且AB=2BC,请在图中按如下要求进行操作和证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).
某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com