
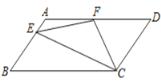
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=![]() ∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
A.(1)(2)B.(1)(2)(4)C.(2)(3)(4)D.(1)(3)(4)
【答案】B
【解析】
利用平行四边形的性质:平行四边形的对边相等且平行,再由全等三角形的判定得出△AEF≌△DMF(ASA),利用全等三角形的性质得出对应线段之间关系进而得出答案.
(1)∵F是AD的中点,
∴AF=FD,
∵在ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=![]() ∠BCD,故正确;
∠BCD,故正确;
(2)延长EF,交CD延长线于M,
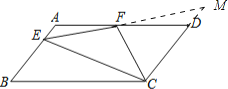
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
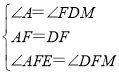 ,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴EF=CF,故正确;
(3)∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
(4)设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故正确,
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明和小亮相约晨练跑步,小明比小亮早1分钟离开家门,3分钟后迎面遇到从家跑来的小亮,两人沿滨江路跑了2分钟后,决定进行长跑比赛,比赛时小明的速度始终是180米/分,小亮的速度始终是220米/分.如图是两人之间的距离y(米)与小明离开家的时间x(分)之间的函数图象,则下列结论中正确的是____________________.(写序号即可)
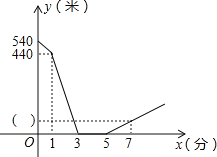
①小明家与小亮家距离为540米;
②小亮比赛前的速度为120米/分;
③小明出发7分钟时,两人距离为80米;
④若小亮从家出门跑了14分钟后,按原路以比赛时的速度返回,则再经过1分钟两人相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.

(1) CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,连接DB,BE,EF,FD.

(1)求证:四边形DBEF是矩形;
(2)如果∠A=60°,DF的长为![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.
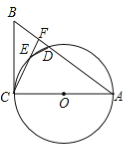
(1)若∠B+∠FED=90°,求证:BC是⊙O的切线;
(2)若FC=6,DE=3,FD=2,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com