
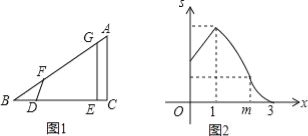
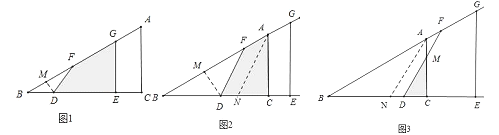
【题目】如图1,△ABC中,∠C=90°,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,1<x≤m,m<x≤3时,函数的解析式不同)
(1)填空:BC的长是 ;
(2)求S关于x的函数关系式,并写出x的取值范围.
【答案】(1)3;(2)S=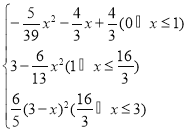 .
.
【解析】
试题分析:(1)由图象即可解决问题.(2)分三种情形:①如图1中,当0≤x≤1时,作DM⊥AB于M,根据S=S△ABC﹣S△BDF﹣S四边形ECAG即可解决.②如图2中,作AN∥DF交BC于N,设BN=AN=x,在RT△ANC中,利用勾股定理求出x,再根据S=S△ABC﹣S△BDF﹣S四边形ECAG即可解决.③如图3中,根据S=![]() CDCM,求出CM即可解决问题.
CDCM,求出CM即可解决问题.
试题解析:(1)由图象可知BC=3.
(2)①如图1中,当0≤x≤1时,作DM⊥AB于M,
由题意BC=3,AC=2,∠C=90°,
∴AB=![]() ,
,
∵∠B=∠B,∠DMB=∠C=90°,
∴△BMD∽△BCA,
∴![]() ,
,
∴DM=![]() ,BM=
,BM=![]() ,
,
∵BD=DF,DM⊥BF,
∴BM=MF,
∴S△BDF=![]() x2,
x2,
∵EG∥AC,
∴![]() ,
,
∴![]() ,
,
∴EG=![]() (x+2),
(x+2),
∴S四边形ECAG=![]() [2+
[2+![]() (x+2)](1﹣x),
(x+2)](1﹣x),
∴S=S△ABC﹣S△BDF﹣S四边形ECAG=3﹣![]() x2﹣
x2﹣![]() [2+
[2+![]() (x+2)](1﹣x)=﹣
(x+2)](1﹣x)=﹣![]() x2+
x2+![]() x+
x+![]() .
.
②如图②中,作AN∥DF交BC于N,设BN=AN=x,
在RT△ANC中,∵AN2=CN2+AC2,
∴x2=22+(3﹣x)2,
∴x=![]() ,
,
∴当1<x≤![]() 时,S=S△ABC﹣S△BDF=3﹣
时,S=S△ABC﹣S△BDF=3﹣![]() x2,
x2,
③如图3中,当![]() <x≤3时,
<x≤3时,
∵DM∥AN,
∴![]() ,
,
∴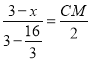 ,
,
∴CM=![]() (3﹣x),
(3﹣x),
∴S=![]() CDCM=
CDCM=![]() (3﹣x)2,
(3﹣x)2,
综上所述S=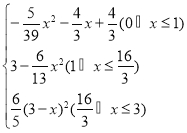 .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 等弧所对的弦相等 B. 平分弦的直径垂直弦并平分弦所对的弧
C. 若抛物线与坐标轴只有一个交点,则b2﹣4ac=0 D. 相等的圆心角所对的弧相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+
x+![]() 与两坐标轴分别交于A、B两点.
与两坐标轴分别交于A、B两点.
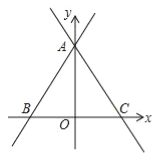
(1)求∠ABO的度数;
(2)过A的直线l交x轴半轴于C,AB=AC,求直线l的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | 12 | n |
B.文学类 | 14 | 35% |
C.艺术类 | m | 20% |
D.其它类 | 6 | 15% |
(1)统计表中的m= ,n= ;
(2)补全条形统计图;
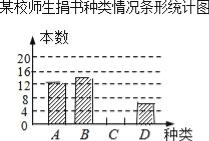
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P(1,﹣4)、Q(m,n)在函数![]() (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
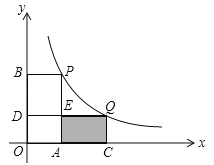
A.减小 B.增大 C.先减小后增大 D.先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,已知A(0,a),B(b,b),C(c,a),其中a,b满足关系式|a-4|+ (b-2)2=0,c=a+b.
(1)求A、B、C三点的坐标,并在坐标系中画出△ABC;
(2)如果在第四象限内有一点P(2,m),请用含m的代数式表示三角形CPO的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com