
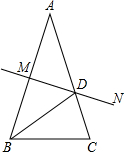
 如图,AB=AC,AB的中垂线MN交AC于点D,交AB于点M,且BC=AD,下列结论中:①△BCD是等腰三角形;②BD平分∠ABC;③∠C=72°;④图中共有3个等腰三角形,其中正确的有( )
如图,AB=AC,AB的中垂线MN交AC于点D,交AB于点M,且BC=AD,下列结论中:①△BCD是等腰三角形;②BD平分∠ABC;③∠C=72°;④图中共有3个等腰三角形,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据线段垂直平分线的性质得到DA=DB,根据等腰三角形的性质、三角形内角和定理计算即可.
解答 解:∵MN是AB的中垂线,
∴DA=DB,
∵BC=AD,
∴BC=BD,即△BCD是等腰三角形,①正确;
∵BC=BD,
∴∠BCD=∠BDC=∠DAB+∠DBA,
∵DA=DB,
∴∠DBA=∠DAB,
∴∠C=2∠DBA,
∵AB=AC,
∴∠ABC=∠C,
∴∠ABC=∠DBA,即BD平分∠ABC,②正确;
设∠A=x,则∠ABC=∠C=2x,
则x+2x+2x=180°,
解得,x=36°,
∴∠C=2x=72°,③正确;
AB=AC、DA=DB,BC=BD,
∴图中共有3个等腰三角形,④正确,
故选:A.
点评 本题考查的是等腰三角形的判定、线段垂直平分线的性质,掌握垂直平分线上任意一点,到线段两端点的距离相等是解题的关键.


科目:初中数学 来源: 题型:解答题
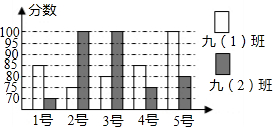 某中学开展“唱红歌”歌唱比赛,九年级(1)班、九年级(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
某中学开展“唱红歌”歌唱比赛,九年级(1)班、九年级(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这个球一定是黑球 | B. | 事先能确定摸到什么颜色的球 | ||
| C. | 这个球可能是白球 | D. | 摸到黑球、白球的可能性大小一样 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当x=2时,$\frac{x+1}{x-2}$的值为零 | |
| B. | 无论x为何有理数,$\frac{3}{{x}^{2}+1}$的值为正数 | |
| C. | 无论x为何值,$\frac{3}{x+1}$的值不可能为正数 | |
| D. | 当x≠3时,$\frac{x-3}{x}$有意义 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com