练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．分解因式：2ax2-8ay2=2a（x+2y）（x-2y）．

    分析 首先提取公因式2a，进而利用平方差公式分解因式得出答案．

    解答 解：原式=2a（x2-4y2）
    =2a（x+2y）（x-2y）．
    故答案为：2a（x+2y）（x-2y）．

    点评 此题主要考查了提取公因式法以及公式法分解因式，熟练应用公式分解因式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．分解因式：-$\frac{1}{4}$x-x3+x2=-x（x-$\frac{1}{2}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

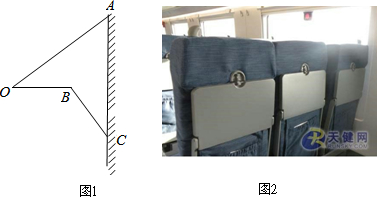
    6．如图所示，某教学活动小组选定测量山顶铁塔AE的高，他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°，在楼顶C测得塔顶A的仰角为36°52′．若小山高BE=62m，楼的底部D与山脚在同一水平面上，求铁塔的高AE．（参考数据：sin36°52′≈0.60，tan36°52′≈0.75）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

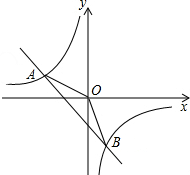    3．如图所示，一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A（-2，n），B（1，-3）两点．
    （1）试确定上述一次函数和反比例函数的表达式；
    （2）求△AOB的面积；
    （3）根据图象直接写出使y1＜y2的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图1，在⊙O中，弦AB⊥弦CD，垂足为点E，连接AC、DB并延长相交于点P，连接AO，DO，AD，BC．
    （1）求证：∠AOD=90°+∠P；
    （2）如图2，若AB平分∠CAO，求证：AD=AB；
    （3）如图3，在（2）的条件下，若OA=5，PB=$\frac{15}{4}$，求四边形ACBD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，“和谐号”高铁列车的小桌板收起时近似看作与地面垂直，小桌板的支架底端与桌面顶端的距离OA=75厘米．展开小桌板使桌面保持水平，此时CB⊥AO，∠AOB=∠ACB=37°，且支架长OB与BC的长度之和等于OA的长度．
    （1）求∠CBO的度数；
    （2）求小桌板桌面的宽度BC．（参考数据sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．先化简，再求值：（$\frac{1}{a-1}-\frac{2}{{a}^{2}-a}$）$÷（a+1-\frac{4a-5}{a-1}）$，其中a是方程x2+2x-3=0的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知直线y=kx+b与x轴、y轴分别交于A、B两点，与反比例函数交于一象限内的P（$\frac{1}{2}$，n），Q（4，m）两点，且tan∠BOP=$\frac{1}{16}$：
    （1）求反比例函数和直线的函数表达式；
    （2）求△OPQ的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．不改变分式的值，使分式$\frac{{\frac{1}{2}{x^2}+\frac{1}{3}}}{{\frac{1}{2}{x^2}-\frac{1}{3}{x^3}}}$的分子和分母各项的系数是整数，化简的结果为（　　）
    A．$\frac{{2{x^2}+3}}{{2{x^2}-3{x^3}}}$B．$\frac{{3{x^2}+2}}{{2{x^2}-3{x^3}}}$C．$\frac{{3{x^2}+2}}{{3{x^2}-2{x^3}}}$D．$\frac{{3{x^2}+2}}{{3{x^3}-2{x^2}}}$

    查看答案和解析>>

    同步练习册答案