练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在平面直角坐标系中,点A、B、C的坐标分别为（2,0）,（3,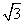）,（1,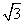）,点D、E的坐标分别为（m,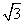m）,（n,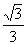n）(m、n为非负数),则CE+DE+DB的最小值是        ．


     4        

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，一次函数y=kx﹣1的图象与x轴交于点A，与反比例函数y=（x＞0）的图象交于点B，BC垂直x轴于点C．若△ABC的面积为1，则k的值是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


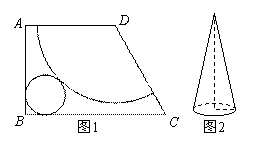
    如图1，已知直角梯形ABCD，∠B=Rt∠。AD=CD=4cm，BC=6cm, 如图在这块铁皮上剪下一个扇形和一个半径为1cm的圆形铁片，使之恰好围成一个图2所示的一个圆锥，则圆锥的高为(　　) 【原创】


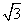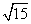    A．cm     B．cm             C．cm       D．cm  


                           

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若一个圆锥侧面展开图的圆心角是270°，圆锥母线l与底面半径r之间的函数关系图象大致是（      ）

    D
     

    A
     

    B
     

    C
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


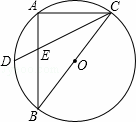
    如图．Rt△ABC内接于⊙O，BC为直径，AB=4，AC=3，D是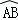的中点，CD与AB的交点为E，则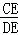等于（　 　）

    A、4          B、3.5            C、3          D、2.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系xOy中，抛物线y=mx2﹣2mx﹣2（m≠0）与y轴交于点A，其对称轴与x轴交于点B．

    （1）求点A，B的坐标；

    （3）若该抛物线在2＜x＜3这一段位于直线AB的下方，

    并且在3＜x＜4这一段位于直线AB的上方，求该抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     若一个正比例函数的图象与一个反比例函数图象的一个交点坐标是(2, 3)，则另一个交点的坐标是（     ）

       A、(2, 3)            B、(3, 2)          C、(, 3)     D、(, )

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：关于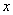的一元二次方程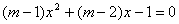（m为实数）

    （1）若方程有两个不相等的实数根，求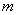的取值范围；

    （2）在（1）的条件下，求证：无论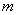取何值，抛物线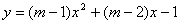总过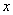轴上的一个固定点；

    （3）若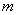是整数，且关于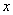的一元二次方程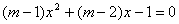有两个不相等的整数根，把抛物线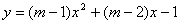向右平移3个单位长度，求平移后的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系xoy中，菱形ABDC的边AB在x轴上，顶点C在y轴上，A（-6,0），C（0,8），抛物线y=ax2﹣10ax+c经过点C，且顶点M在直线BC上，则抛物线解析式为                   ；若点P在抛物线上且

    满足S△PBD=S△PCD，则点P的坐标为                  。

     


    查看答案和解析>>

    同步练习册答案