
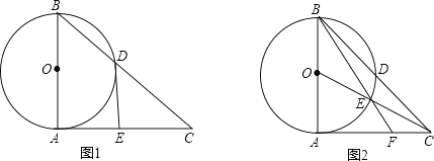
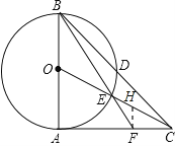
【题目】以△ABC的边AB为直径作⊙O交BC于D.
(1)如图1,过点D作⊙O的切线交AC于E,若点E为线段AC中点,求证:AC与⊙O相切.
(2)在(1)的条件下,若BD=6,AB=10,求△ABC的面积.
(3)如图2,连OC交⊙O于E,BE的延长线交AC于F,若AB=AC,CE=AF=4,求CF的长.
【答案】(1)见解析;(2)![]() ;(3)CF=
;(3)CF=![]()
【解析】
(1)连接OD,OE,利用全等三角形的判定得出△ODE与△OAE全等,再利用切线的判定证明即可;
(2)根据切线的性质和勾股定理和三角形面积公式解答即可.
(3)由△AEC∽△EFC即可得出FC的长.
证明:(1)连接OD,OE,AD,
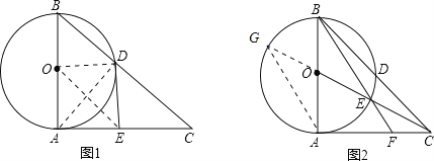
∵AB为直径,
∴∠ADB=90°,
∴∠ADC=90°,
∵点E为线段AC中点,
∴AE=EC,
∴AE=DE,
在△ODE与△OAE中
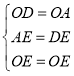 ,
,
∴△ODE≌△OAE(SSS),
∴∠ODE=∠OAE,
∵⊙O的切线交AC于E,
∴∠ODE=90°,
∴∠OAE=90°,
∴OA⊥AC,
即AC与⊙O相切;
(2)如图3,连接AD,AE
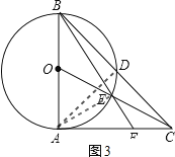
∵△ABD∽△ADC
∴![]() =
=![]() =
=![]()
∴![]() =
=![]() =
=![]()
∴CD=![]() ,AC=
,AC=![]()
∴S△ABC=![]() =
=![]() =
=![]() ;
;
(3)如图,作FH∥AB交OC于H,设半径为r
△FEH为等腰三角形
∵AC=AB=2r
∴CF=2r-4
∵△CFH∽△OAC
∴![]()
∴HF=r-2
∴EH=r-2
∴HC=4-(r-2)=6-r
∵△CFH∽△OAC
∴![]()
∴![]()
∴r=1±![]()
∴r=1+![]()
∴CF=2r-4=2![]() -2.
-2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
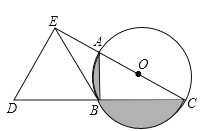
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
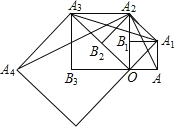
【题目】如图,四边形 OAA1B1 是边长为 1 的正方形,以对角线 OA1 为边作第二个正方形 OA1A2B2,连接 AA2,得到△ AA1A2;再以对角线 OA2 为边作第三个正方形 OA2A3B3,连接 A1A3,得到△A1A2A3;再以对角线 OA3 为边作第 四个正方形,连接 A2A4,得到△A2A3A4……记△AA1A2、△A1A2A3、△A2A3A4 的面积分别为 S1、S2、S3,如此下 去,则 S2019=_____ .
查看答案和解析>>
科目:初中数学 来源: 题型:
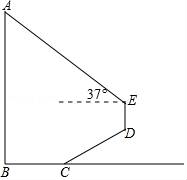
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
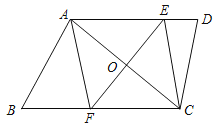
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连结AF、CE.
(1)求证:△AOE≌△COF.
(2)试判断四边形AFCE的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,y=ax2+bx+c的图象经过点(﹣1,0),(m,0);有如下判断:①abc<0;②b>3c;③![]() =1﹣
=1﹣![]() ;④|am+a|=
;④|am+a|=![]() .其中正确的判断有( )
.其中正确的判断有( )
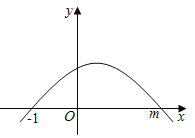
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如下表:
产品 | 每件售价(万元) | 每件成本(万元) | 每年其他费用(万元) | 每年最大产销量(万元) |
甲 | 10 | a | 40 | 200 |
乙 | 18 | 8 | 40+0.05x2 | 100 |
其中a为常数,且5≤a≤8.
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() ,
,![]() 两种产品共10件,其生产成本和利润如下表.
两种产品共10件,其生产成本和利润如下表.
|
| |
成本(万元 | 2 | 5 |
利润(万元 | 1 | 3 |
(1)若工厂计划获利14万元,问![]() ,
,![]() 两种产品应分别生产多少件?
两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于22万元,问工厂有哪几种生产方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com