
 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )| A. | 2,$\frac{π}{3}$ | B. | 2$\sqrt{3}$,π | C. | $\sqrt{3}$,$\frac{2π}{3}$ | D. | 2$\sqrt{3}$,$\frac{4π}{3}$ |
分析 如图,连接OB、OC.首先证明△OBC是等边三角形,求出BC、BM,根据勾股定理即可求出OM,利用弧长公式求出$\widehat{BC}$的长即可.
解答 解:如图,连接OB、OC.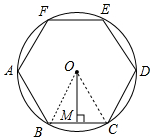
∵ABCDEF是正六边形,
∴∠BOC=60°,OB=OC=4,
∴△OBC是等边三角形,
∴BC=OB=OC=4,
∵OM⊥BC,
∴BM=CM=2,
在Rt△OBM中,OM=$\sqrt{O{B}^{2}-B{M}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
$\widehat{BC}$的长=$\frac{60π•4}{180}$=$\frac{4}{3}$π.
故选D.
点评 本题考查正多边形与圆、等边三角形的性质、勾股定理、弧长公式等知识,解题的关键是记住等边三角形的性质,弧长公式,属于基础题,中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
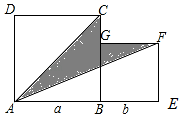 如图,正方形ABCD和正方形BEFG平放在一起.
如图,正方形ABCD和正方形BEFG平放在一起.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 160° | B. | 150° | C. | 120° | D. | 110° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
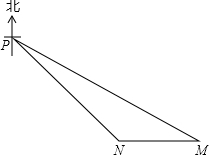 如图,某海岛上有一观测点P,一天上午9:00观测到一轮船在点M处,M在观测点P南偏东60°方向上,渔船由东向西匀速航行跟踪鱼群,当天上午9:30渔船行至点N处,N在观测点P的东南方向上,已知该渔船的速度为每小时40海里.
如图,某海岛上有一观测点P,一天上午9:00观测到一轮船在点M处,M在观测点P南偏东60°方向上,渔船由东向西匀速航行跟踪鱼群,当天上午9:30渔船行至点N处,N在观测点P的东南方向上,已知该渔船的速度为每小时40海里.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com