
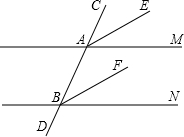
 解:已知,AM∥BN,AE为∠CAM的平分线,BF为∠ABN的平分线,如图所示,
解:已知,AM∥BN,AE为∠CAM的平分线,BF为∠ABN的平分线,如图所示, ∠CAM,∠ABF=
∠CAM,∠ABF= ∠ABN(角平分线定义),
∠ABN(角平分线定义),

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
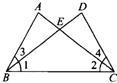 20、如图所示,已知:①AE=DE,②∠1=∠2,③∠3=∠4,将其中的两个作为条件,另一个作为结论,写出一个真命题加以证明.
20、如图所示,已知:①AE=DE,②∠1=∠2,③∠3=∠4,将其中的两个作为条件,另一个作为结论,写出一个真命题加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:
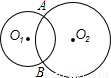
 如图;⊙Ol、⊙O2相交于点A、B,现给出4个命题:
如图;⊙Ol、⊙O2相交于点A、B,现给出4个命题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:新课标九年级数学竞赛培训第23讲:圆与圆(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com