
 如图:在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,若OA、OB的长分别是方程若x2-7mx+48=0的两根且OB>OA,AB=10.AC平分∠BAO交x轴于点C.
如图:在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,若OA、OB的长分别是方程若x2-7mx+48=0的两根且OB>OA,AB=10.AC平分∠BAO交x轴于点C.分析 (1)由一元二次方程根与系数的关系,结合AB的长,利用勾股定理可求得m的值,进一步可求得OA、OB的值,则可求得A、B的坐标;
(2)过C点作AB的垂线交AB于点M,可证得△OAC≌△MAC,在Rt△BCM中,由勾股定理可求得OC的长,可求得C点坐标,利用待定系数法可求得直线AC的解析式;
(3)由条件只能有∠APB=90°和∠PBA=90°,可设出P点坐标,分别表示出PA、PB和AB,利用勾股定理可列出方程,可求得P点坐标.
解答 解:
(1)x2-7mx+48=0的两根是OA、OB,
∴OA+OB=7m,OA•OB=48,
∵OA2+OB2=100,
∴(OA+OB)2-2OA•OB=100,即49m2-96=100,解得m=2或m=-2(舍去),
∴x2-14x+48=0,解得x1=6,x2=8,
∴OA=6,OB=8,
∴A(0,6),B(8,0);
(2)过C点作AB的垂线交AB于点M,如图,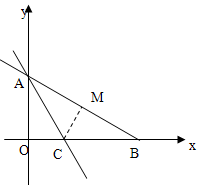
∵AC平分∠BAO,
∴∠OAC=∠CAB,
在△OAC和△MAC中
$\left\{\begin{array}{l}{∠OAC=∠CAB}\\{∠AOC=∠AMC}\\{AC=AC}\end{array}\right.$
∴△OAC≌△MAC(AAS),
∴CM=CO,AM=AO,
∵BC2=CM2+MB2
∴OC=3,
∴C(3,0),
设直线AC的解析式为y=kx+b(k≠0,k、b为常数),
代入A(6,0)C(3,0)得$\left\{\begin{array}{l}{b=6}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$,
∴直线AC的解析式为y=-2x+6;
(3)存在.
∵点P在直线AC上,
∴可设P(x,-2x+6),
∵A(0,6),B(8,0),
∴PA2=x2+(-2x+6-6)2=5x2,PB2=(x-8)2+(-2x+6)2=5x2-40x+100,且AB2=100,
∵∠BAC<90°,
∴当△PAB为直角三角形时,有∠APB=90°和∠PBA=90°,
①当∠APB=90°时,则有PA2+PB2=AB2,即5x2+5x2-40x+100=100,解得x=0(与A重合,舍去)或x=4,此时P点坐标为(4,-2);
②当∠PBA=90°时,则有PB2+AB2=PA2,即5x2-40x+100+100=5x2,解得x=5,此时P点坐标为(5,-4);
∴P点坐标为(4,-2)或(5,-4).
点评 本题为一次函数的综合应用,涉及一元二次方程根与系数的关系、全等三角形的判定和性质、待定系数法、勾股定理、方程思想和分类讨论思想等知识.在(1)中求得m的值是解题的关键,在(2)中证得△OAC≌△MAC是解题的关键,在(3)中确定出直角顶点是解题的关键,注意分两种情况.本题考查知识点较多,综合性较强,难度适中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
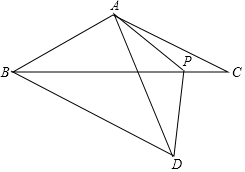 如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.
如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com