
【题目】完成下面推理过程:
如图,∠1+∠2=230°,b∥c,则∠1,∠2,∠3,∠4各是多少度?
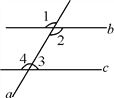
解:∵∠1=∠2(__________________),
∠1+∠2=230°,
∴∠1=∠2=___________(填度数).
∵b∥c,
∴∠4=∠2=_______(填度数)(_______________________________),
∠2+∠3=180°(________________________________),
∴∠3=180°-∠2=____________(填度数).
科目:初中数学 来源: 题型:
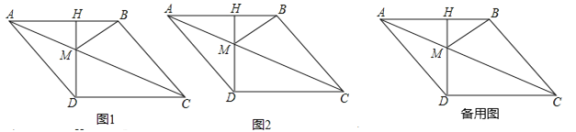
【题目】如图1,四边形ABCD是菱形,AD=10,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=6.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经市场调研发现:某品牌童装平均每天可售出 20 件,每件盈利 40元.在每件降价幅度不超过 18 元的情况下,若每件童装降价 1 元,则每天可多售出 2 件,设降价 x 元.
(1)降价 x 元后,每件童装盈利是多少元,每天销售量是多少件;
(2)要想每天销售这种童装盈利 1200 元,那么每件童装应降价多少元?
(3)每天能盈利 1800 元吗?如果能,每件童装应降价多少元?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
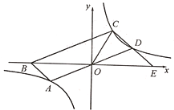
【题目】如图,在平面直角坐标系中,平行四边形ABCD的边AD经过O点,A、C、D三点都在反比例函数![]() 的图像上,B点在
的图像上,B点在![]() 轴的负半轴上,延长CD交
轴的负半轴上,延长CD交![]() 轴于点E,连接CO.
轴于点E,连接CO.
若C(1,2),D(2,1),则![]() 为_______.
为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校办公楼前有一长为m,宽为n的长方形空地,在中心位置留出一个直径为2b的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.

(1)用含字母和π的式子表示出阴影部分的面积S;
(2)当m=8,n=6,![]() 时,阴影部分的面积是多少?(π取3)
时,阴影部分的面积是多少?(π取3)
查看答案和解析>>
科目:初中数学 来源: 题型:
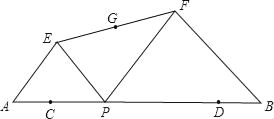
【题目】如图,已知AB=12,点C,D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,①△EFP的外接圆的圆心为点G;②四边形AEFB的面积不变;③EF的中点G移动的路径长为4;④△EFP的面积的最小值为8.以上说法中正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
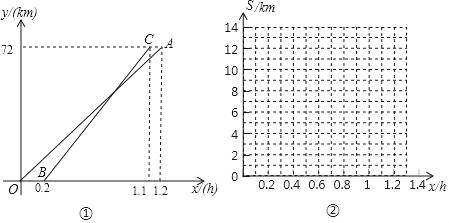
【题目】甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲坐地铁先出发,甲出发0.2小时后乙开汽车前往.设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km).如图①是y1与y2关于x的函数图象.
(1)分别求线段OA与线段BC所表示的y1与y2关于x的函数表达式;
(2)当x为多少时,两人相距6km?
(3)设两人相距S千米,在图②所给的直角坐标系中画出S关于x的函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
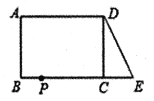
【题目】已知:如图,在长方形![]() 中,
中,![]() ,
,![]() .延长
.延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿
出发,以每秒2个单位的速度沿![]() 向终点
向终点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒,当
秒,当![]() 的值为___________时,
的值为___________时,![]() 和
和![]() 全等.
全等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com